Analysieren, Interpolieren und Extrapolieren von Mensurwerten

© Arndt Brünner, Gelnhausen  • Version: 8. Januar 2003  •  Mensurenrechner  • Beziér-Interpolation •  Übersicht

Anleitung:

  1. Gegebene Maße in die Tabelle eintragen, alternativ über ein Textfeld oder komplett über die Zwischenablage
  2. Art der zu suchenden Funktion angeben
    Es wird automatisch nach der besten derartigen Funktion gesucht. Der Wert bei Standardabweichung (möglichst klein) ist ein Maß dafür, wie gut die Funktion die gegebenen Werte annähert. Wählen Sie bei Durchmesserangaben zuerst "Exponentialfunktion + Konstante".
  3. Optionen wählen
  4. Button Analyse betätigen
  5. Dem Autor eine eMail mit Ihren Eindrücken über diese Seite schicken

¯ Erläuterungen der Optionen und Funktionen ¯

Es stehen einige ¯ Mensurbeispiele zum Ausprobieren ¯ bereit.
¯ Hier ¯ finden Sie einige zusätzliche Erläuterungen zum Verständnis der Analyseergebnisse.
TasteMaß
C0
Cis0
D0
Dis0
E0
F0
Fis0
G0
Gis0
A0
B0
H0
c0
cis0
d0
dis0
e0
f0
fis0
g0
gis0
a0
b0
h0
c1
cis1
d1
dis1
e1
f1
fis1
g1
gis1
a1
b1
h1
c2
cis2
d2
dis2
e2
f2
fis2
g2
gis2
a2
b2
h2
c3
cis3
d3
dis3
e3
f3
fis3
g3
gis3
a3
b3
h3
c4

Dieses Programm analysiert Verlaufsmensuren von Orgelpfeifen und berechnet alle fehlenden Werte gemäß der besten gefundenen Mensurkurve.

Zu suchende Funktionsart:
Beachten Sie bitte, daß für die gewählte Funktionsart mindestens Werte gegeben sein müssen. Andernfalls kann der Algorithmus keine sinnvolle Funktion finden.
Berechnete Maße runden auf Dezimalstelle(n).
Darstellung von Dezimalbrüchen in der Ausgabe
Registerfußzahl (für die Berechnung der Abweichung vom Normmaß) andere: 
Normmensur-Abweichung anzeigen
Analysebereich:
Zusätzliche Ausgabe der berechneten Werte über ein Textfeld zum Kopieren
    

Nach der Analyse werden die Ergebnisse in eine neu erzeugte html-Seite geschrieben.
Falls Sie alsbald nach Betätigen der Taste eine Java-Script-Fehlermeldung erhalten, versuchen Sie es bitte einfach noch einmal.


Erläuterungen

Geben Sie bekannte Mensurmaße in die Textfelder der Tabelle neben den zugehörigen Tastennamen ein. Oft sind nur einige Maße, z.B. die aller C-Pfeifen, bekannt. In den meisten Fällen reichen diese Maße jedoch völlig aus, um die zugrundeliegende Mensurkurve zu ermitteln und zu analysieren - falls sie existiert.

Sie können eine vorhandene Mensurtabelle auch komplett über ein Eingabefeld im unteren Bereich der Seite importieren.

Es können Durchmessermaße und rechteckige Querschnittsmaße eingegeben werden. Bei letzteren verwenden Sie bitte den Schrägstrich als Trennung zwischen den Längen (Bsp.: 195.2/147.5). Rechteckige Querschnitte werden intern in Durchmessermaße flächengleicher runder Querschnitte umgerechnet. Die Ausgabe erfolgt (bislang) unabhängig von der Eingabe in jedem Fall in Durchmessermaßen.
Bei Dezimalbrüchen kann hier auch das Dezimalkomma (statt des Dezimalpunkts) verwendet werden.

Mensursprünge werden prinzipiell nicht als solche erkannt, da der Algorithmus davon ausgeht, daß die gebauten und gemessenen Mensurmaße von den mathematisch-geometrischen Planungen abweichen. Sprungstellen werden daher zunächst als Abweichungen von einer virtuellen Sollkurve interpretiert. Das Programm erkennt zwar an den Analyseergebnissen, daß eventuell ein Mensursprung vorliegt und wird in einer späteren Version auch auch die Stelle benennen, kann und wird aber keine Teilbereiche automatisch separat analysieren. Sie können in einem solchen Fall jedoch den Analysebereich einschränken und die Verlaufsmensur stückweise manuell analysieren.

Der Analysealgorithmus (Gaußsche Methode der »kleinsten Fehlerquadrate«) sucht nach Funktionen, durch die die gegebenen Punkte möglichst gut approximiert werden. Bau- oder meßtechnisch bedingte Abweichungen und Ungenauigkeiten der Maße fallen daher nicht ins Gewicht und beeinflussen das Auffinden einer zugrundeliegenden Regelmäßigkeit kaum oder gar nicht! Daher gilt, nahezu unabhängig von der Güte der einzelnen Messungen:

Je mehr Maße eingetragen werden, desto besser ist die Analyse.

Da – namentlich historischen – Mensurmaßen oftmals geometrische Reihen zugrunde liegen, bei denen sich die Mensurmaße, abzüglich eines bestimmten Wertes, der geheimnisvoll arcanum genannt wurde, nach einer konstanten Anzahl von Halbtönen halbieren, kann nach geeigneten Exponentialfunktionen zur Basis 2 gesucht werden, die einen konstanten oder wahlweise linearen Anteil (Gerade) besitzen:

f(x) = k·2(-x/a) + c     oder     f(x) = k·2(-x/a) + b·x + c

Die Variable x in den Funktionen repräsentiert die Nummer der Pfeife (0=C, 1=Cis, 11=c, 23=c1 usw.). Entscheidend ist nun, wie die Größe a gewählt werden muß, so daß 2x/a den Mensurverlauf möglichst gut approximiert. Die Zahl a ist dann das Maß für jenes Intervall, das der Mensurverlaufsplanung zugrunde lag. Von ihr läßt sich auf das Mensurverhältnis zweier im Oktavabstand stehender Pfeifen schließen. Es ist 1 : 2 –12/a.
Im ersten Funktionsterm repräsentiert c das sogenannte arcanum, das Geheimnis der Mensur.

Ein freier Mensurverlauf (ohne Sprünge) kann innerhalb des Definitionsbereichs oftmals sehr gut durch Polynome vom Grad 1 (Gerade), 2 (Parabel) oder 3 (kubische Parabel) approximiert werden, die im Falle von quadratischen und kubischen Parabeln jedoch außerhalb des gegebenen Bereichs selten über einen interessanten Bereich "stabil" bleiben und sich somit – ganz im Gegensatz zu Exponential-Approximierungen – nur in sehr bedingtem Maße zur Extrapolation eignen.

Nach Betätigung des Analyse-Buttons wird eine neue Seite erzeugt, in der abhängig von den gewählten Einstellungen Art und Details des gefundenen Mensurverlaufs sowie eine komplette Mensurliste ausgegebenen werden.
Wenn nur eine einzelne Funktion berechnet wurde (Funktionsart genau angeben, Anzahl der besten Funktionen auf 1 oder manuell mit Angabe einer Teilung), finden Sie optional im unteren Bereich der Seite ein Textfeld, in dem die komplette Maßtabelle ein weiteres Mal erscheint. Sie können dieses Feld verwenden, um die Werte mit Kopieren und Einfügen in ein eigenes Tabellenblatt zu übernehmen. Den Funktionsterm können Sie direkt aus dem oberen Bereich der Seite kopieren.
Wählen Sie bitte die Art des gewünschten Dezimalkommas (, oder .).

­ Zur Eingabe der Optionen ­  |   ¯ Weitere Erläuterungen zu den Analyseergebnissen ¯

Direkte Eingabe und Einfügen einer Tabellenspalte aus der Zwischenablage

  

Hier können Sie die Tabellenwerte nach den u.a. Regeln alternativ eingeben oder eine schon vorher erstellte einspaltige Tabelle über der Zwischenablage einfügen. Beachten Sie aber bitte die notwendige Formatierung:

Es werden zwei Arten der Formatierung unterstützt:

  1. Die Mensurwerte müssen bei der ersten Art voneinander durch Zeilenvorschübe getrennt sein, d.h. alle Werte müssen separat und in eigenen Zeilen stehen. Sie können somit etwa eine Spalte aus einer EXCEL-Tabelle übernehmen.
    Beachten Sie, daß jeder Taste eine Zeile entsprechen muß. Wenn nur die C-Pfeifen-Maße importiert werden, müssen zwischen den Werten jeweils 11 Zeilen (für die Maße für cis-h) leer bleiben. Geben Sie hierzu noch die tiefste Taste des eingefügten Wertebereichs ein:
  2. Die Mensurwerte können auch in dieser Art übergeben werden:
    C0:141,7 c0:79,8 c1:43,7 c2:24,7 c3:14,6
    Zwischen Tastenangabe und Mensurmaß muß sich ein Doppelpunkt (alternativ: Tabulatorzeichen) befinden, das Trennzeichen zwischen den Wertepaaren ist das Leerzeichen (alternativ Semikolon oder Zeilenvorschub).

Zu den Optionen  |   Zum Analysebutton  |   Zum Tabellenkopf  |   zurück

Beispiele zum Ausprobieren

Zum Ausprobieren und Testen dieses Programmes stehen einige Mensuren der Silbermannorgel in Freiberg/Sachsen zur Verfügung. Klicken Sie bitte hierauf, um die Mensuren im unteren Teil dieses Fensters anzuzeigen, wenn sie nicht schon sichtbar sind.

Dort können Sie auf die als Verweis gekennzeichneten Mensurmaße klicken. Diese werden dann automatisch (ohne Meldung) in die Tabelle übernommen. Auch die Registerfußzahl wird eingetragen. Zum Ausprobieren eines weiteren Beispiels müssen Sie zunächst über die entsprechenden Verweise zum Eingabefenster zurückkehren.

Sie schließen das untere Fenster mit einem Klick hierauf (Achtung: Alle Eingaben gehen dabei verloren).


Erläuterung der Analyseergebnisse

Im Kopfbereich der Ergebnisseite findet sich typischerweise eine solche Tabelle:

Nr. Art  Teilung   arca-
num 		 Oktav-
 teilung 		 Standard-
 abweichung 		  Funktionsterm 
1 Exp+Const ~ reine Undezime
1750 Cent		 3 1 : 1,6085
» gold. Schnitt (1,618)		 3,616587,65141*2^(-x/17,5) + 2,9661

Diese Angaben bedeuten folgendes:

Nr.
Für späteren Gebrauch, im Moment immer 1
Art
Die gewählte Funktionsart. Im Beispiel eine Exponentialfunktion mit Additionskonstante
Teilung
Gibt an, in welchem konstanten Abstand sich die Mensurmaße nach Abzug der Additionskonstante (=arcanum) halbieren (bzw. verdoppeln). Der Algorithmus sucht in 10 Cent-Intervallen nach der besten Funktion. 100 Cent entsprechen einem gleichschwebend gestimmten Halbton, 1200 Cent einer Oktave. Die Intervallangaben beruhen auf zu Hundert gerundeten Centwerten.
Diese Angabe kann natürlich nur bei Exponentialfunktionen gemacht werden.
Die Oktavteilung errechnet sich aus dem Centwert c der Teilung. Sie ist 1 : 21200/c
Siehe auch bei Oktavteilung
arcanum
Die Additions-"konstante" bei Exponentialfunktionen. Bei Exponentialfunktionen mit Gerade findet sich hier der lineare Anteil, also der Term, der die addierte Gerade erzeugt
Oktavteilung
Gibt an, in welchem Verhältnis sich die Mensurmaße nach Abzug der Additionskonstante (bzw. des linearen Anteils) bei Pfeifen im Oktavabstand zueinander verhalten. Die Teilung (s.o.) in Cent ergibt sich aus der Oktavteilung 1:t durch 1200·ln(2)/ln(t)
Typische Werte sind:
Standardabweichung
Maß für die "Streuung" der gegebenen Werte um die gefundene Funktion. Je kleiner dieser Wert, desto besser ist die gefundene Funktion. Die Abweichung im Beispiel ist kaum noch tolerabel!
Der Analysealgorithmus findet die Funktion mit der kleinsten Standardabweichung automatisch.
Funktionsterm
Die gefundene Funktion in "computerlesbarer" Form. Dieser Funktionsterm kann markiert, kopiert und etwa in MS-EXCEL direkt verwendet werden werden. Der Term im Beispiel (87,65141*2^(-x/17,5) + 2,9661) bedeutet:

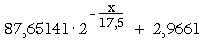
Die Variable x steht für die Tastennummer, beginnend mit x=0 für C0. Bei der Verwendung in EXCEL kann das x leicht durch die aktuelle Zeilennummer abzüglich der Zeilennummer der Zeile für C0 ersetzt werden, z.B.:
=87,65141*2^(-(ZEILE()-5)/17,5) + 2,9661
wenn die Maße für C0 in der 5. Zeile stehen.

Wahl der Funktion im Hinblick auf die Absicht der Analyse

Wenn Sie historische Mensuren analysieren, ist im Grunde nur die Einstellung Exponentialfunktion mit Konstante interessant. Das rechnerische Ergebnis der Exponentialfunktion mit Konstante entspricht der geometrischen Konstruktion der Mensurmaße mithilfe eines "Mensurdreiecks" (siehe etwa bei Dom Bédos). Der addierte Festwert entspricht dem arcanum bei der Exponentialfunktion mit Konstante, die Einteilung des Dreiecks in Oktaven genau der Oktavteilung (hier 1:2):

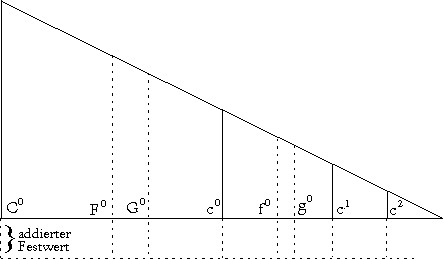
Mensurdreieck nach Dom Bédos und Wolfgang Adelung

Der Einstellung Exponentialfunktion mit Gerade würde in dieser geometrischen Planung keine leicht aus der Horizontalen genommene Gerade als Additionswertlieferant entsprechen, sondern eine exponentiell verlaufende Kurve.

Wenn Sie Mensuren analysieren, um zu gegebenen Maßen eine Ergänzung von Pfeifen vornehmen zu können, empfiehlt es sich, wenn mit den Exponentialfunktionen keine geeignete Kurve gefunden werden kann, es entweder mit den Parabeltypen zu versuchen und/oder nur Werte im Bereich der Ergänzung einzugeben (mindestens drei oder vier stehenlassen).

Bei gewünschter Extrapolation sind Parabeln weitgehend ungeeignet, da sie "ihrer Natur entsprechend" nicht den Gesetzmäßigkeiten eines Mensurverlaufs folgen. Außerhalb des durch die gegebenen Werte abgesteckten Bereichs sind die durch Parabeln extrapolierten Werte ungeeignet! Verwenden Sie Exponentialfunktionen, so können Sie bei sinnvollen Werten für Oktavteilung und Standardabweichung (s.o.) auch große Bereiche extrapolieren.

­ Zur Eingabe der Optionen ­  |   ­ Zum Analysebutton ­

Anmerkungen des Autors

Der Wunsch nach einem Programm zum Interpolieren von Mensurdaten wurde von einigen Arbeitskreismitgliedern gleich nach Veröffentlichung des Mensurrechners geäußert. In der Regel werden fehlende Mensurwerte durch einfaches Anwenden einer fortgesetzten Multiplikation mit einem geeigneten Faktor berechnet, es entsteht also eine geometrische Reihe, deren Verlauf nur von den zwei Eckpunkten abhängt. Dieses Verfahren wird in meinen Augen jedoch in den seltensten Fällen einer gegebenen Mensur gerecht, da es den Tonumfang in Teile zerlegt, die nach den separaten Interpolationsvorgängen nicht mehr einer gemeinsamen Kurve gehorchen. Es sei denn, die Eckdaten folgen denselben einfachen Gesetzen. Historische Mensuren erfüllen diese Voraussetzung jedoch sehr selten, obgleich sie in vielen und prominenten Fällen sehr wohl einer komplizierteren (und bewußt dadurch verborgenen?) Konstruktionsregel folgen. Das Wörtchen "arcanum", das die alten Orgelbauer im Zusammenhang mit diesen Regeln prägten, heißt eben Geheimnis und drückt somit aus, daß den Mensurwerten eine Regel zugrundeliegt, die alles andere als offensichtlich ist.

Lange Zeit konnten die Herleitungsverfahren für die Mensurwerte und damit die "erzeugenden mathematischen Funktionen" nur empirisch durch vergleichendes Ausprobieren ermittelt werden. Ein großes Problem bei der Erkundung der zugrundeliegenden mathematischen Funktion ist die Ungenauigkeit der Maße, die baubedingt oft im "Zickzack" von der idealen Mensurlinie abweichen. Bereits Carl Friedrich Gauß (Braunschweig 30. 4. 1777 - Göttingen 23. 2. 1855), deutscher Mathematiker, Astronom und Physiker, schuf allerdings die mathematischen Voraussetzungen für schnelle Computeralgorithmen zur Analyse von (namentlich fehlerbehafteten) Meßwerten durch Finden geeigneter Funktionen, die die Werte am besten approximieren.

Das Programmieren eines schnellen Analyseprogramms für das Internet, d.h. in Javascript, hat einige Zeit in Anspruch genommen und jede Menge Mühe gekostet, nicht zuletzt da es neben einem anstrengenden Beruf geschehen mußte, der in letzter Zeit nicht viel Zeit und Muße ließ. Nun funktioniert es und ermöglicht u.a. wunderbar schnelles Analysieren von historischen Mensuren. Silbermannsche Aliquoten sind z.B. offensichtlich in der Regel im Goldenen Schnitt mensuriert. Alle testweise eingegebenen Mensuren von Registern dieser Art bestätigten diese These.

Ich bin sehr gespannt auf Ihre Reaktion, denn ich denke, es ist etwas Neuartiges, was Sie hier zum Nulltarif ausprobieren und verwenden können.

Bitte schicken Sie mir jederzeit willkommene Anregungen (und noch viel willkommenere Anerkennungen) per eMail: arndt.bruenner@t-online.de