Lösungen zum Test vom 3. 4. 2003

zu Aufgabe: 1 2 3 4 5

Aufgabe 1

Von rechtwinkligen Dreiecken sind die folgenden Größen bekannt:

	Gruppe A		Gruppe B
	(1) a=37°, b=90°, b=591cm		a=30°, b=90°, b=519cm
	(2) a=8cm, b=10cm, g=90°		a=15cm, b=12cm, g=90°
	(3) a=90°, g=85°, a=46m		a=90°, g=80°, a=56m

Berechnen Sie die übrigen Strecken und Winkel. Berechnen Sie außerdem h_c des zweiten Dreiecks!

Lösungen

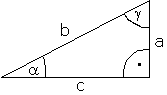
(1)		Sinus = Gegenkathete / Hypotenuse Gegenkathete = Hypotenuse·Sinus a = b·sin(a) Gruppe A: a = 591cm · sin(37°) = 355,67...cm Gruppe B: a = 519cm · sin(30°) = 259,5cm Kosinus = Ankathete/Hypotenuse Ankathete = Hypotenuse·Kosinus c = b·cos(a) Gruppe A: c = 591cm · cos(37°) = 471,99...cm Gruppe B: c = 519cm · cos(30°) = 449,467...cm g = 180° - a - b Gruppe A: g = 180° - 37° - 90° = 53° Gruppe B: g = 180° - 30° - 90° = 60°

(2)		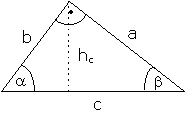Hypotenuse² = Summe der Kathetenquadrate (Pythagoras) Gruppe A: c = Ö(8² + 10²) = 12,80624847...cm Gruppe B: c = Ö(15² + 12²) = 19,2093727...cm Tangens = Gegenkathete/Ankathete tan(a) = a/b a = tan^-1(a/b) Gruppe A: a = tan^-1(8/10) = 38,6598...° Gruppe B: a = tan^-1(15/12) = 51,34...° oder a = sin^-1(a/c) oder a = cos^-1(b/c) b = 180° - 90° - a = Gruppe A: b = 180° - 90° - 38,6598...° = 51,34..° Gruppe B: b = 180° - 90° - 51,34...° = 38,6598...° h_c = b·sin(a) Gruppe A: h_c = 8cm·sin(38,6598...°) = 6,24695...cm Gruppe B: h_c = 12cm·sin(51,34...°) = 9,37...cm

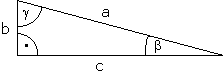
(3)		b = a · cos(g) Gruppe A: b = 46cm · cos(85°) = 4,00916...cm Gruppe B: b = 56cm · cos(80°) = 9,7242979...cm c = a · sin(g) Gruppe A: a = 46cm · sin(85°) = 45,824956...cm Gruppe B: a = 56cm · sin(80°) = 55,14923...cm b = 180° - a - g Gruppe A: b = 5° Gruppe B: b = 10°

zu Aufgabe: 1 3 4 5

Aufgabe 2

a)	Berechnen Sie die Steigungswinkel der linearen Funktionen - Gruppe A: f(x)=2x-6 und g(x)=-0,5x+3. - Gruppe B: f(x)=-2x+6 und g(x)=0,5x-3.
b)	Geben Sie, möglichst ohne die Funktionen zu zeichnen, an, in welchem Winkel sich die beiden zugehörigen Geraden schneiden.

Lösung

Der Steigungswinkel a berechnet sich durch den Arkustangens der Steigung m.

Gruppe A: a_f = tan^-1(2) » 63,435° a_g = tan^-1(-0,5) » -26,565°

Gruppe B: a_f = tan^-1(-2) » -63,435° a_g = tan^-1(0,5) » 26,565°

Der Schnittwinkel der beiden Geraden ist die Differenz der Steigungswinkel: 63,435° - (-26,565°) = 90°

Das wird deutlich, wenn man sich die Graphen anschaut (Graphen von Gruppe B):

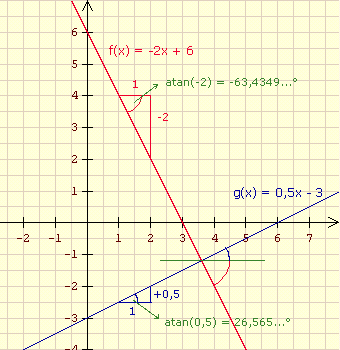
zu Aufgabe: 1 2 4 5

Aufgabe 3

Eine der steilsten Straßen in Gelnhausen ist der Johanniterweg mit 27% Steigung (siehe Foto rechts). Vom Schild bis zum Eingang des im Hintergrund sichtbaren Hauses sind es 55m (Gruppe A) bzw. 50m (Gruppe B) Fußweg.

Skizzieren Sie die Situation und berechnen Sie die Höhendifferenz!

Lösung

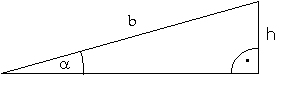
a = atan(27%) = atan(0,27) = 15,1095751...°

Gruppe A: h = 55m · sin(a) = 14,33662...m
Gruppe B: h = 50m · sin(a) = 13,03329...m

zu Aufgabe: 1 2 3 5

Aufgabe 4

Im Jahre 1173 wurde mit dem Bau des Turmes von Pisa begonnen, der sich schon bald wegen des sandigen Untergrunds zur Seite neigte.

Der Wissenschaftler Galileo Galilei wurde im Jahre 1564 in Pisa geboren. Er berichtete, daß er den Schiefen Turm für eines seiner physikalischen Experimente benutzt hat. (Siehe Pressefoto rechts.)
Er ließ Gegenstände von der obersten Galerie fallen, um zu demonstrieren, daß die Fallgeschwindigkeit unabhängig vom Gewicht des fallenden Gegenstandes ist.

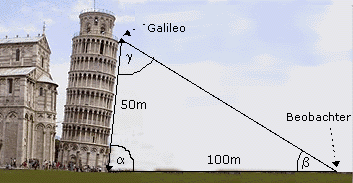
Ein Beobachter steht 100m vom Fußpunkt des Turmes entfernt und sieht Galileo unter dem Winkel von 27,6°.

a)	Berechnen Sie den Neigungswinkel des Turmes!
b)	Berechnen Sie, wie weit der Gegenstand vom Fußpunkt des Turmes entfernt aufschlägt, den Galileo soeben losläßt!

Lösung

Verwende den Sinussatz, um zunächst g zu berechnen:

    b         c
  —————  =  —————            | · sin b  · sin b
  sin b     sin g

  b · sin g  =  c · sin b    | : a

            c · sin b
  sin g  =  —————————   
                b

           c · sin b
  g = sin^-1 —————————
               b

           100m · sin 27,6°
  g = sin^-1 ————————————————  =  67,9096632870975...°
                 50m

  a = 180° - 27,6° - 67,9096632870975° = 84,49...°

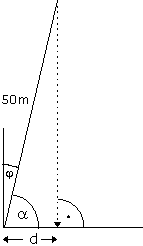
Der Neigungswinkel j ist eigentlich die Differenz zur Senkrechten, also j = 90° - 84,49° = 5,51°

Die Entfernung d des Aufschlagspunktes vom Fußpunkt des Turms berechnet sich so:
d = 50m · cos a » 4,8m

Der Turm hängt also fast 5m über!

zu Aufgabe: 1 2 3 4

Aufgabe 5

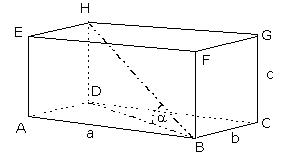
Berechnen Sie den Neigungswinkel der Raumdiagonalen BH in diesem Quader:

Gruppe A: a=10m, b=7m, c=8,6m

Gruppe B: a=10m, b=7,6m, c=8m

Lösung

Der gesuchte Winkel ist das Verhältnis zwischen den Längen von Gegenkathete DH und Ankathete BD des rechtwinkligen Dreiecks DBH

Berechne zunächst die Länge der Diagonalen BD mit Pythagoras:
Gruppe A: |BD| = Ö(10² + 7²) = 12,2065556157337...m
Gruppe B: |BD| = Ö(10² + 7,6²) = 12,5602547744861...m

Nun berechne den Winkel mit dem Arkustangens von |DH|/|BD|:
Gruppe A: a = atan(8,6m/12,21m) = 35,2°
Gruppe B: a = atan(8m/12,56m) = 32,5°