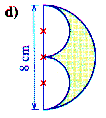Hilfe zur Lösung der Nr. 23 aus dem Buch

Aufgabe a)

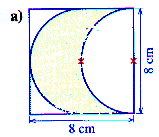
Fläche Denke das Quadrat in eine linke und eine rechte Hälfte zerteilt. Es entstehen zwei Rechtecke mit den Seiten 8 cm und 4 cm. Die beiden "Kreisspitzen" im rechten Teil (es sind genaugenommen zwei Viertelkreise) passen genau in die "Aussparungen" im linken Teil. Damit ist die gefragte Fläche gleich der Fläche des Rechtecks 8 cm · 4 cm = 32 cm2
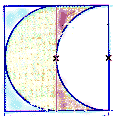Umfang Die Zerteilung hilft auch beim Berechnen des Umfangs: Im linken Teil liegt ein Halbkreisbogen mit dem Radius 4 cm. Im rechten Teil liegen ein gleichgroßer Halbkreisbogen und zusätzlich oben und unten zwei Strecken mit der Länge 4 cm. Damit besteht der Umfang der Figur aus dem Umfang des Kreises (mit r = 4 cm) plus 8 cm.

Aufgabe b)

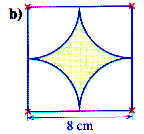
Umfang Denke die Figur in vier Quadranten unterteilt. In jedem Quadranten liegt ein Viertelkreisbogen. Damit ist der Umfang der Figur gleich dem Umfang des Kreises mit r = 4 cm.
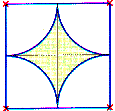Fläche Auch die vier (weißen) Viertelkreisflächen ergeben zusammen die Fläche eines Kreises mit r = 4 cm. In der Figur wird genau diese Fläche in dem umschließenden Quadrat mit den Seitenlängen 8 cm ausgespart. Damit ist die Fläche der Figur die Fläche des Quadrates (64 cm2) abzüglich der Fläche des Kreises (p·42).

Aufgabe c)

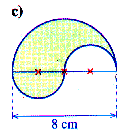
Fläche Der linke kleine Halbkreis (blau, r=2) paßt genau in die Aussparung rechts (grün), daher ist die Fläche der Figur die Fläche des Halbkreises mit r=4.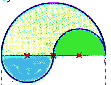
Umfang Der Umfang der Figur setzt sich zusammen aus dem oberen großen Halbkreisbogen mit r=4 und zwei kleinen Halbkreisbögen unten mit r=2, also u=p·8/2 + 2·p·4/2 = p·4 + p·4 = 8 p Beachte, daß oberer und unterer Teil jeweils 4p lang sind. Damit sind beide "bogenmäßigen Überbrückungen" des Durchmessers gleich lang. Das gilt als Regel für alle derartigen Teilungen.

Aufgabe d)

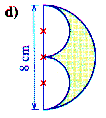
Umfang

Auch hier setzt sich der Umfang aus einem großen Halbkreisbogen mit r=4 und zwei kleinen Halbkreisbögen mit r=2 zusammen. Damit ist der Umfang der Figur d) gleich dem Umfang der Figur c).

Fläche

Zur Berechnung der Fläche ziehe von der Fläche des großen Halbkreises mit r=4 zweimal die Fläche des kleinen Halbkreises mit r=2 (bzw. einmal die Fläche des kompletten Kreises mit r=2) ab.

Aufgabe e)

Ab hier wird im Buch der Radius nicht mehr numerisch genannt, sondern nur noch mit r bezeichnet. Gehen wir dennoch davon aus, daß der Radius wie bei den Aufgaben a)-d) r = 4 cm ist.

Umfang

Die Figur wird umschrieben durch einen Halbkreisbogen in der oberen Hälfte mit r=4 und zwei Viertelkreisbögen (entspricht einem Halbkreisbogen) mit auch jeweils r=4 in der unteren Häfte. Damit ist u = p·4 + p·4 = 8p

Fläche

Zur Berechnung der Fläche zerteilen wir die Figur in der Mitte horizontal in oben und unten.
Oben ist ein Halbkreis mit r = 4 und unten ein Rechteck mit A=8·4=32, dem die Fläche zweier Viertelkreise mit r=4 fehlt. Die beiden Viertelkreise entsprechen zusammen in ihrer Fläche dem oberen Halbkreis.
A = A_Halbkreis + (A_Rechteck - A_Halbkreis)
= A_Rechteck = 32 cm²

Aufgabe f)

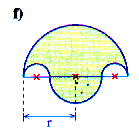
Umfang

Nach der Regel entspricht die Länge der drei kleinen Halbkreisbögen unten der Länge des großen Halbkreisbogens oben. Damit ist der Umfang gleich dem Umfang des Kreises mit r = 4.

Die beiden kleinen Halbkreise links unten und rechts unten haben r=1 und damit die Gesamtlänge eines ganzen Kreisumfangs mit r=1, u=2p.
Der mittlere Halbkreisbogen unten hat r=2 und damit ebenfalls u=2p.
Zusammen ist das für die untere Hälfte der Figur also 4p, und das ist auch der Umfang des oberen großen Halbkreisbogens mit r=4.

Fläche

Berechne die Fläche des oberen Halbkreises (r=4) und ziehe die beiden Halbkreise (r=1) ab. Addiere den Halbkreis unten Mitte mit r=2.

Aufgabe g)

Obere und untere Hälfte der Figur sind identisch (gehen durch Drehung um 180° um den Mittelpunkt auseinander hervor). Damit genügt es, für Fläche und Umfang jeweils eine Hälfte zu berechnen und zu verdoppeln.

Achtung: Der Radius des umhüllenden Kreises (r=4) wird hier in drei Teile zerlegt! Die äußeren Halbkreise (Außenbegrenzungen der Figur) haben damit 2/3 des Radius' des großen Kreises, also 4·2/3 = 8/3; die kleineren Halbkreise (Innenbegrenzungen der Figur) haben den 1/3-fachen Radius des großen Kreises, also 4·1/3 = 4/3

Fläche

Berechne die Fläche des Halbkreises mit r=8/3 und subtrahiere die Fläche des Halbkreises mit r=4/3. Verdopple das Ergebnis.

Umfang

Addiere die Kreisumfänge der Kreise mit r=8/3 (zwei Außenhalbkreise) und r=4/3 (zwei Innenhalbkreise).

Aufgabe h)

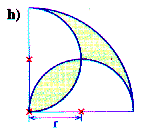
Umfang Der Umfang der Figur besteht aus zwei Halbkreisbögen mit r=4 und einem Viertelkreisbogen mit r=8.
Fläche Zur Berechnung der Fläche zerteile die "Linse" unten links der Länge nach in zwei Hälften. Diese passen genau in die "Aussparungen" des sichelförmigen Figurteiles oben rechts, wodurch eine Figur entsteht, die viel leichter zu berechnen ist. Es ist ein Viertelkreis mit r=8, dem ein rechtwinkliges, gleichschenkliges Dreieck mit der Fläche 8·8/2=32 herausgeschnitten wurde.

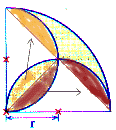So. Ich hoffe, damit ist euch zunächst mal geholfen. Außerdem wünsche ich euch erfolgreiches Üben und dennoch ein erholsames Wochenende.

Fragen, Hinweise (Fehler?) und Anregungen gerne und jederzeit an arndt.bruenner@t-online.de
 
Hier findet ihr Allgemeines zum Kreis.