Lösungen zur 4. Arbeit vom 8. Februar 2002
Nr. 1 | Nr. 2 | Nr. 3
| Nr. 4 | Nr. 5 | Nr. 6 |
zurück
1. Aufgabe
Gib p und q dieser Gleichungen an und überprüfe mit dem Satz von Vieta, ob die angegebenen Lösungsmengen zutreffen!
Gruppe A:
| a) | | x² + 5,5x - 7 = 0 |
| L = { -2 ; 3,5 } |
| b) | | x² + x = 20 | | L = { -5 ; 4 } |
Gruppe B:
| a) | | x² + 5,5x + 7 = 0 |
| L = { 2,5 ; 3 } |
| b) | | x² - x = 20 | | L = { 5 ; -4 } |
Lösung
Die erste Gleichung ist jeweils in der Normalform gegeben, die zweite muß zunächst in diese umgeformt werden.
Gruppe A
a)
q = x1 · x1 = -2 · 3,5 = -7
-p = x1 + x1 = -2 + 3,5 = 1,5
p = -1,5
Normalform der Gleichung, die die angegebenen Lösungen hat: x² - 1,5x - 7 = 0
Die angegebene Gleichung hat somit nicht diese Lösungsmenge.
b)
q = -5 · 4 = -20
-p = -5 + 4 = -1
p = 1
Normalform der Gleichung, die die angegebene Lösungsmenge hat: x² + x - 20 = 0
Die angegebene Gleichung ist dazu äquivalent, hat also die gegebene Lösungsmenge.
Gruppe B
a)
q = x1 · x1 = 2,5 · 3 = 7,5
-p = x1 + x1 = 2,5 + 3 = 5,5
p = -5,5
Normalform der Gleichung, die die angegebenen Lösungen hat: x² - 5,5x + 7,5 = 0
Die angegebene Gleichung hat somit nicht diese Lösungsmenge.
b)
q = 5 · (-4) = -20
-p = 5 + (-4) = 1
p = -1
Normalform der Gleichung, die die angegebene Lösungsmenge hat: x² - x - 20 = 0
Die angegebene Gleichung ist dazu äquivalent, hat also die gegebene Lösungsmenge.
zurück
Aufgabe 2
Gib quadratische Gleichungen mit den angegebenen Lösungsmengen an
Gruppe A
a) L = { 3 ; 6 }
b) L = { 0 ; 17 } c) L = { -5 }
Satz von Vieta anwenden:
p = -( x1 + x2 )
q = x1 · x2
a) p = -9 q = 18 x² - 9x + 18 = 0
b) p = -17 q = 0 x² - 17x = 0
c) p = 10 q = 25 x² + 10x + 25 = 0
Gruppe B
a) L = { 3 ; 7 }
b) L = { 0 ; 13 } c) L = { -3 }
Satz von Vieta anwenden:
p = -( x1 + x2 )
q = x1 · x2
a) p = -10 q = 21 x² - 10x + 21 = 0
b) p = -13 q = 0 x² - 13x = 0
c) p = 6 q = 9 x² + 6x + 9 = 0
zurück
Aufgabe 3
Löse diese Gleichungen sowohl mit quadratischer Ergänzung als auch mit der p-q-Formel
Gruppe A
a)
x² - 18x = -81 | + 81
x² - 18x + 81 = 0
Lösen mit p-q-Formel:
p = -18 q = 81
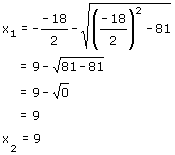 L = { 9 }
Lösen mittels quadratischer Ergänzung:
x² - 18x + 81 = 0 | - 81
x² - 18x = -81 | + 81 ( = (18/2)²)
x² - 18x + 81 = 0
(x - 9)² = 0 | Ö
x - 9 = 0 | + 9
x = 9
L = { 9 }
b)
2x² - 2x - 7,5 = 0 | :2
x² - x - 3,75 = 0
Lösen mit p-q-Formel:
p = -1 q = -3,75
L = { 9 }
Lösen mittels quadratischer Ergänzung:
x² - 18x + 81 = 0 | - 81
x² - 18x = -81 | + 81 ( = (18/2)²)
x² - 18x + 81 = 0
(x - 9)² = 0 | Ö
x - 9 = 0 | + 9
x = 9
L = { 9 }
b)
2x² - 2x - 7,5 = 0 | :2
x² - x - 3,75 = 0
Lösen mit p-q-Formel:
p = -1 q = -3,75
 L = { -1,5 ; 2,5 }
Lösen mittels quadratischer Ergänzung:
x² - x - 3,75 = 0 | + 3,75
x² - x = 3,75 | + 0,25 ( = (-1/2)² )
x² - x + 0,25 = 4 |
(x - 0,5)² = 4 | Ö
x - 0,5 = 2 v x - 0,5 = -2 | + 0,5
x = 2,5 v x = -1,5
L = { -1,5 ; 2,5 }
L = { -1,5 ; 2,5 }
Lösen mittels quadratischer Ergänzung:
x² - x - 3,75 = 0 | + 3,75
x² - x = 3,75 | + 0,25 ( = (-1/2)² )
x² - x + 0,25 = 4 |
(x - 0,5)² = 4 | Ö
x - 0,5 = 2 v x - 0,5 = -2 | + 0,5
x = 2,5 v x = -1,5
L = { -1,5 ; 2,5 }
Gruppe B
a)
x² + 36 = 12x | - 12x
x² - 12x + 36 = 0
Lösen mit p-q-Formel:
p = -12 q = 36
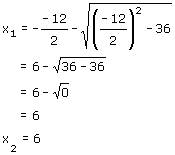 L = { 6 }
Lösen mittels quadratischer Ergänzung:
x² - 12x + 36 = 0 | - 36
x² - 12x = -36 | + 36 ( = (12/2)²)
x² - 12x + 36 = 0
(x - 6)² = 0 | Ö
x - 6 = 0 | + 6
x = 6
L = { 6 }
L = { 6 }
Lösen mittels quadratischer Ergänzung:
x² - 12x + 36 = 0 | - 36
x² - 12x = -36 | + 36 ( = (12/2)²)
x² - 12x + 36 = 0
(x - 6)² = 0 | Ö
x - 6 = 0 | + 6
x = 6
L = { 6 }
b)
2x² + 6x - 3,5 = 0 | :2
x² + 3x - 1,75 = 0
Lösen mit p-q-Formel:
p = 3 q = -1,75
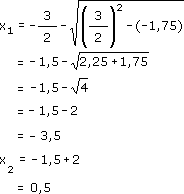 L = { -3,5 ; 0,5 }
Lösen mittels quadratischer Ergänzung:
x² + 3x - 1,75 = 0 | + 1,75
x² + 3x = 1,75 | + 2,25 ( = (-3/2)² )
x² + 3x + 2,25 = 4 |
(x + 1,5)² = 4 | Ö
x + 1,5 = 2 v x + 1,5 = -2 | + 1,5
x = 0,5 v x = -3,5
L = { -3,5 ; 0,5 }
L = { -3,5 ; 0,5 }
Lösen mittels quadratischer Ergänzung:
x² + 3x - 1,75 = 0 | + 1,75
x² + 3x = 1,75 | + 2,25 ( = (-3/2)² )
x² + 3x + 2,25 = 4 |
(x + 1,5)² = 4 | Ö
x + 1,5 = 2 v x + 1,5 = -2 | + 1,5
x = 0,5 v x = -3,5
L = { -3,5 ; 0,5 }
zurück
Aufgabe 4
Löse diese Gleichungen mit p-q-Formel oder quadratischer Ergänzung
Gruppe A
a)
(x - 3)(3 - x) = 6x - 2
3x - x² - 9 + 3x = 6x - 2 | -6x +2
-x² - 7 = 0 | ·(-1)
x² + 7 = 0
p = 0 q = 7
D = 0 - 7 = -7 < 0 Þ L = { } keine Lösung
b)
9 8
————— - ——— = -1 | ·(x + 1)
x + 1 x
8x + 8
9 - ———————— = -x - 1 | ·x
x
9x - 8x - 8 = -x² - x | +x² +x
x² + 2x - 8 = 0 | +9
x² + 2x + 1 = 9
(x + 1)² = 9
x + 1 = 3 v x + 1 = -3
x = 2 v x = -4
Gruppe B
a)
(x - 3)(3 - x) = 5x - 3
3x - x² - 9 + 3x = 5x - 3 | -5x +3
-x² + x - 6 = 0 | ·(-1)
x² - x + 6 = 0
p = -1 q = 6
D = 1 - 6 = -5 < 0 Þ L = { } keine Lösung
b)
5 8
——— + ————— = -1 | ·(x - 6)
x x - 6
5x - 30
————————— + 8 = -x + 6 | ·x
x
5x - 30 + 8x = -x² - 6x | +x² +6x
x² + 7x - 30 = 0
p = 7 q = -30
x1 = -3,5 - Ö(12,25 + 30)
= -3,5 - Ö42,25
= -3,5 - 6,5 = -10
x2 = -3,5 + 6,5 = 3
zurück
Aufgabe 5
Was ist und wozu dient die Diskriminante einer quadratischen Gleichung?
Gib auch ein Beispiel!
Die Diskriminante ist der Ausdruck unter der Wurzel der p-q-Formel (p²/4-q). Sie dient der Unterscheidung, wieviele Lösungen eine quadratische Gleichung
besitzt. Ist sie größer 0, dann hat die Gleichung zwei Lösungen, ist sie gleich 0, hat die Gleichung nur eine, ist sie kleiner 0, hat die Gleichung keine Lösung.
Beispiele:
x² + 3x - 20 = 0 D = 3²/4 + 20 = 22,25 > 0 Þ zwei Lösungen
x² + 3x + 20 = 0 D = 3²/4 - 20 = -17,75 < 0 Þ keine Lösung
x² + 6x + 9 = 0 D = 6²/4 - 9 = 0 Þ eine Lösung
zurück
Aufgabe 6
Gruppe A
Jeder Würfel hat 6 quadratische Seitenflächen. Bei einem Würfel der Kantenlänge a hat jede Seitenfläche den Flächeninhalt a².
Gesucht ist der Würfel, dessen Gesamtoberfläche sich um 576cm² vergrößert, wenn sich die Kantenlänge verdoppelt und dann noch um 1cm vergrößert.
Anleitung: Setze x als Kantenlänge des Würfels. Überlege, wie groß die Kantenlänge des vergrößerten Würfels ist (mit x ausgedrückt).
Stelle eine Gleichung auf, bei der links der um 576cm² vergrößerte Flächeninhalt des kleinen und rechts der Flächeninhalt des neuen Würfels mit der größeren Kantenlänge steht.
Lösung
Die Oberfläche des Würfels besteht aus 6 Quadraten der Fläche x², beträgt also 6x². Die um 1 vergrößerte doppelte
Kantenlänge ist 2x+1, eine Fläche (2x+1)² und die Gesamtoberfläche 6(2x+1)². Die Gleichung lautet damit:
6x² + 576 = 6(2x + 1)²
6x² + 576 = 6(4x² + 4x + 1)
6x² + 576 = 24x² + 24x + 6 | -24x² -24x -6
-18x² - 24x + 570 = 0 | :(-18)
x² + 4/3x - 95/3 = 0
19
x = - ———— v x = 5
3
Da die negative Lösung ausscheidet, ist die Kantenlänge des gesuchten Würfels 5cm.
Gruppe B
Jeder Würfel hat 6 quadratische Seitenflächen. Bei einem Würfel der Kantenlänge a hat jede Seitenfläche den Flächeninhalt a².
Gesucht ist der Würfel, dessen Gesamtoberfläche sich um 270cm² vergrößert, wenn sich die Kantenlänge verdreifacht und dann noch um 1cm vergrößert.
Anleitung: Setze x als Kantenlänge des Würfels. Überlege, wie groß die Kantenlänge des vergrößerten Würfels ist (mit x ausgedrückt).
Stelle eine Gleichung auf, bei der links der um 270cm² vergrößerte Flächeninhalt des kleinen und rechts der Flächeninhalt des neuen Würfels mit der größeren Kantenlänge steht.
Lösung
Die Oberfläche des Würfels besteht aus 6 Quadraten der Fläche x², beträgt also 6x². Die um 1 vergrößerte dreifache
Kantenlänge ist 3x+1, eine Fläche (3x+1)² und die Gesamtoberfläche 6(2x+1)². Die Gleichung lautet damit:
6x² + 270 = 6(3x + 1)²
6x² + 270 = 6(9x² + 6x + 1)
6x² + 270 = 54x² + 36x + 6 | -54x² -36x -6
-48x² - 36x + 264 = 0 | :(-48)
x² + 0,75x - 5,5 = 0
x = - 2,75 v x = 2
Da die negative Lösung ausscheidet, ist die Kantenlänge des gesuchten Würfels 2cm.
zurück
Ergebnisse
Punkteverteilung:
| Aufgabe | Punkte |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 6 |
| 5 | 4 |
| 6 | Zusatz-
aufgabe |
|
Notenspiegel:
Durchschnitt: 3,8
30,4% negative Noten
|
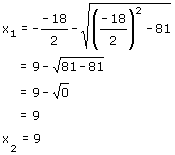 L = { 9 }
Lösen mittels quadratischer Ergänzung:
x² - 18x + 81 = 0 | - 81
x² - 18x = -81 | + 81 ( = (18/2)²)
x² - 18x + 81 = 0
(x - 9)² = 0 | Ö
x - 9 = 0 | + 9
x = 9
L = { 9 }
b)
2x² - 2x - 7,5 = 0 | :2
x² - x - 3,75 = 0
Lösen mit p-q-Formel:
p = -1 q = -3,75
L = { 9 }
Lösen mittels quadratischer Ergänzung:
x² - 18x + 81 = 0 | - 81
x² - 18x = -81 | + 81 ( = (18/2)²)
x² - 18x + 81 = 0
(x - 9)² = 0 | Ö
x - 9 = 0 | + 9
x = 9
L = { 9 }
b)
2x² - 2x - 7,5 = 0 | :2
x² - x - 3,75 = 0
Lösen mit p-q-Formel:
p = -1 q = -3,75
 L = { -1,5 ; 2,5 }
Lösen mittels quadratischer Ergänzung:
x² - x - 3,75 = 0 | + 3,75
x² - x = 3,75 | + 0,25 ( = (-1/2)² )
x² - x + 0,25 = 4 |
(x - 0,5)² = 4 | Ö
x - 0,5 = 2 v x - 0,5 = -2 | + 0,5
x = 2,5 v x = -1,5
L = { -1,5 ; 2,5 }
L = { -1,5 ; 2,5 }
Lösen mittels quadratischer Ergänzung:
x² - x - 3,75 = 0 | + 3,75
x² - x = 3,75 | + 0,25 ( = (-1/2)² )
x² - x + 0,25 = 4 |
(x - 0,5)² = 4 | Ö
x - 0,5 = 2 v x - 0,5 = -2 | + 0,5
x = 2,5 v x = -1,5
L = { -1,5 ; 2,5 }
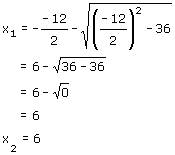 L = { 6 }
Lösen mittels quadratischer Ergänzung:
x² - 12x + 36 = 0 | - 36
x² - 12x = -36 | + 36 ( = (12/2)²)
x² - 12x + 36 = 0
(x - 6)² = 0 | Ö
x - 6 = 0 | + 6
x = 6
L = { 6 }
L = { 6 }
Lösen mittels quadratischer Ergänzung:
x² - 12x + 36 = 0 | - 36
x² - 12x = -36 | + 36 ( = (12/2)²)
x² - 12x + 36 = 0
(x - 6)² = 0 | Ö
x - 6 = 0 | + 6
x = 6
L = { 6 }
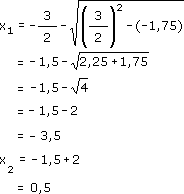 L = { -3,5 ; 0,5 }
Lösen mittels quadratischer Ergänzung:
x² + 3x - 1,75 = 0 | + 1,75
x² + 3x = 1,75 | + 2,25 ( = (-3/2)² )
x² + 3x + 2,25 = 4 |
(x + 1,5)² = 4 | Ö
x + 1,5 = 2 v x + 1,5 = -2 | + 1,5
x = 0,5 v x = -3,5
L = { -3,5 ; 0,5 }
L = { -3,5 ; 0,5 }
Lösen mittels quadratischer Ergänzung:
x² + 3x - 1,75 = 0 | + 1,75
x² + 3x = 1,75 | + 2,25 ( = (-3/2)² )
x² + 3x + 2,25 = 4 |
(x + 1,5)² = 4 | Ö
x + 1,5 = 2 v x + 1,5 = -2 | + 1,5
x = 0,5 v x = -3,5
L = { -3,5 ; 0,5 }