 Neu
Neu
Man kann bei Rechtecken mit dem Seitenverhältnis 1:x stets ein kleineres Rechteck abtrennen, das dasselbe Seitenverhältnis hat. Teilt man das kleinere wieder und auch dieses und so fort, so ziehen sich die Rechtecke immer dichter an einen Punkt zusammen, der s/(q²+1) vom linken bzw. oberen Rand des größten Rechtecks entfernt liegt, wobei q=1/x und s=jeweilige Seitenlänge. Die zwei diagonal gegenüberliegenden Eckpunkte der Rechtecke, die |
Beim Seitenverhältnis des Rechteckes von 1:x = 1:1,538862030494607660840461... berührt die Spirale die Rechteckseiten
lediglich, ohne sie zweimal zu schneiden. Der Wert ist die Lösung der Gleichung
Herleitung:
Logarithmische Spiralen besitzen die allgemeine Polarkoordinatengleichung
Gewinnung von k aus x: Da der Radius bei einer Umdrehung um den Faktor x4 zunimmt, muß gelten:
r·x4 = a·ek·(j+2p) | :x4
r = a·x-4·ek·(j+2p)
r = a·eln(x^-4)·ek·(j+2p)
r = a·eln(x^-4)+k·(j+2p)
r = a·eln(x^-4)+kj+2pk
Wegen r=a·ekj (siehe oben) gilt: kj = ln(x^-4)+kj+2pk, und damit ist:
k = -ln(x-4)/(2p) = 2·ln(x)/p
und der Schnittwinkel t = atan(p/(2·ln(x))
Nun betrachten wir den Fall, daß die Kurve in E die Gerade FG gerade berührt, also ihre Tangente den Winkel t zur Radialen ME bildet.
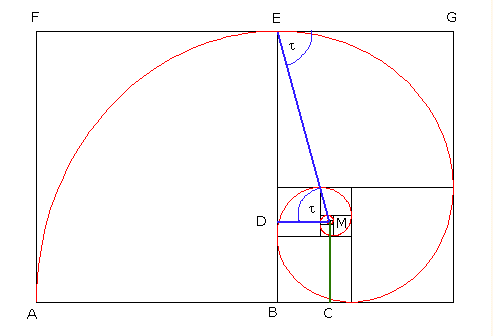
Wenn |FG| = x und |AF| = 1, dann ist |AC| = x/(1/x²+1), |DE| = 1/(1/x²+1), |EG| = 1/x, |AB| = x - 1/x und somit |BC| = |AC| - |AB| = x/(1/x²+1) - (x - 1/x) = 1/(x³ + x)
Dann ist
Wegen t=atan(1/k)= atan(p/(2·ln(x4)), muß in diesem
Falle gelten: p/(2·ln(x)) = x³ oder eben