Der Kosinussatz

Matheseiten-Übersicht
Dreiecksberechnung
Sinussatz
zurück

Der Kosinussatz

Der Kosinussatz wird auch als trigonometrischer Pythagoras bezeichnet. Das rührt daher, daß mit ihm wie beim Satz des Pythagoras eine fehlende Dreieckseite berechnet werden kann, allerdings im Gegensatz zum Pythagoras, der ja nur für rechtwinklige Dreiecke gilt, in jedem beliebigen Dreieck.

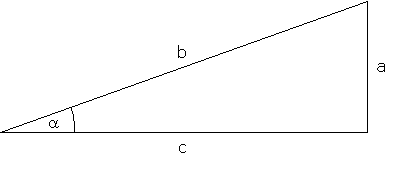
Man kann ja ein Dreieck eindeutig konstruieren, wenn man zwei Seiten und den eingeschlossenen Winkel gegeben hat (Kongruenzsatz SWS). Also zum Beispiel die Seiten b und c und den Winkel α in diesem Dreieck:

Die Seite a ist durch b, c und α eindeutig bestimmt!

Der Kosinussatz dient nun dazu, die Länge der Seite a rechnerisch zu bestimmen. Das kommt in der "Wirklichkeit" sehr häufig vor, z.B. bei Höhen- und Entfernungsbestimmungen.

Vorüberlegungen

Bevor ich zeige, wie man das mit den trigonometrischen Funktionen Sinus und Kosinus bewerkstelligen kann, sind einige Vorüberlegungen nötig.

Die Winkelfunktionen Sinus und Kosinus gelten ja bekanntlicherweise nur im rechtwinkligen Dreieck:

Die beiden Funktionen sind dabei so definiert:

und

Bei den trigonometrischen Funktionen gelten verschiedene interessante Rechengesetze. Das wichtigste und vielleicht schönste davon ist folgende Regel:
( sin(α) )² + ( cos(α) )² = 1

Um das zu beweisen, muß man für sin und cos jeweils die Definitionen mit den Dreiecksseiten einsetzen und den Term auflösen. Dabei muß beachtet werden, daß das zugrundeliegende Dreieck rechtwinklig ist mit b als Hypotenuse.
Daher gilt: b² = a² + c²

Somit ergibt sich folgende Vereinfachung des Termes:

Der Kosinussatz

Damit man die trigonometrischen Funktionen in einem nichtrechtwinkligen Dreieck anwenden kann, benutzt man eine Hilfskonstruktion: Man konstruiert die Höhe vom Punkt C auf die Seite c:

Dadurch wird die Seite c in die zwei Abschnitte p und q zerteilt, und es entstehen zwei rechtwinklige Dreiecke, die die Seite h gemeinsam haben. (Das folgende gilt aufgrund dieser Konstruktion vorerst auch nur für diesen Fall, daß nämlich die Höhe innerhalb des Dreiecks liegt.)

Zur Erinnerung: Das Ziel ist, eine Formel zu finden, mit der a berechnet werden kann, wenn b, c und α gegeben sind.

α und b liegen im linken Dreieck, a liegt im rechten, c ist die Summe jeweils einer Kathete beider Dreiecke.

Die Idee ist nun, die beiden Dreiecke durch ihre gemeinsame Größe h rechnerisch zu "verbinden", um mit den gegebenen Größen zur Größe a zu gelangen.

Im rechten Dreieck gilt (Pythagoras): h² = a² – q²

Im linken Dreieck bringt man den gegebenen Winkel α ins Spiel und berechnet: h = b · sin(α)

Da uns h letztlich nicht interessiert, kann die zweite Gleichung dazu verwendet werden, h² in der ersten Gleichung zu ersetzen. Nach der zweiten Gleichung gilt nämlich: h² = ( b · sin(α) )² = b² · (sin(α))²

So kann man die beiden Gleichungen gleichsetzen, wobei h² letztlich verschwinden kann:

b² · (sin(α))² = h² = a² – q²

b² · (sin(α))² = a² – q²

In dieser Gleichung sind α und b bekannt, a soll berechnet werden, nur das q stört noch! Um das q rauszuschmeißen, überlegt man sich, daß p + q = c gilt. Also ist q = c – p

Außerdem gilt: p = b · cos(α).

Somit gilt: q = c – b · cos(α).

Hier ist q nur mit bekannten Größen umschrieben worden! Uff! soweit gut, aber jetzt kommt noch der

Endspurt!

Nun muß nur noch dieser Term ( c – b · cos(α) ) für q in die Gleichung b² · (sin(α))² = a² – q² eingesetzt werden, und schon haben wir eine Gleichung, in der nur noch a unbekannt ist!

b² · (sin(α))² = a² – ( c – b·cos(α) )²

Zuerst wird die Klammer mit dem Quadrat rechts aufgelöst (2. binomische Formel):

b² · (sin(α))² = a² – ( c² – 2·b·c·cos(α) + b²·(cos(α))² )

Dann wird die Minusklammer aufgelöst:

b² · (sin(α))² = a² – c² + 2·b·c·cos(α) – b²·(cos(α))²

Nun wird die Gleichung nach a² umgeformt:

a² = c² – 2·b·c·cos(α) + b²·(cos(α))² + b² · (sin(α))²

Das b² wird ausgeklammert:

a² = c² – 2·b·c·cos(α) + b²· [ (cos(α))² + sin(α))² ]

Nach obiger Regel gilt: (cos(α))² + (sin(α))² = 1
und somit ist:

a² = c² – 2·b·c·cos(α) + b²

Man zieht das b² nach vorne und erhält damit den

Kosinussatz
a² = b² + c² – 2 b c cos(α)

Die Sache wird übrigens etwas überschaubarer, wenn man die Gleichung b² · (sin(α))² = a² – q² gleich nach a² auflöst und dann erst q² ersetzt. Dann fällt das fehlerträchtige Auflösen der Minusklammer weg.

Bislang ist der Satz bewiesen für die Dreiecke, bei denen β<90° ist. Zu beweisen bleibt daher β=90° und β>90°.

Der Fall β=90° (siehe Abbildung rechts) ist schnell bewiesen: Im hier vorliegenden rechtwinkligen Dreieck ist b die Hypotenuse, c die Ankathete und a die Gegenkathete zu α, es gilt also:

In diesem Fall kann man im Kosinussatz a² = b² + c² - 2bc cos α anstelle von cos α folglich c/b schreiben, womit sich ergibt: a² = b² + c² - 2c², bzw. vereinfacht a² = b² - c²; und das ist der Satz von Pythagoras a² + c² = b² für dieses Dreieck.
Wenn a und c einen stumpfen Winkel bilden, d.h. wenn β>90° ist und die Höhe h auf c außerhalb des Dreiecks liegt (siehe Abbildung rechts), ergibt sich für h² aus der jeweiligen Anwendung des Satzes von Pythagoras auf die beiden enthaltenen rechtwinkligen Dreiecke:

   h² = a² - q² = a² - (p - c)²
   h² = b² - p²

Gleichsetzen ergibt

   a² - (p - c)² = b² - p²
   a² - (p² - 2cp + c²) = b² - p²
   a² - p² + 2cp - c² = b² - p²
   a² + 2cp - c² = b²

Wegen cos(α) = p/b ist p = b·cos(α) und man kann in der letzten Gleichung ersetzen:

   a² + 2c·b·cos(α) - c² = b²

Hieraus folgt sofort:

   a² = b² + c² - 2bc·cos(α)