Gruppe a
Löse das Gleichungssystem durch das Einsetzungsverfahren:
| 6x + y = 12 | |
|
| -3y – 12x = -21 |
Nr. 1 | Nr. 2 | Nr. 3 |
Nr. 4 | Nr. 5 | Nr. 6 |
Bewertung und Ergebnis |
zurück | eMail
Rechner für lineare Gleichungssysteme |
Übersicht Matheseiten |
Gästebuch
Gruppe a:
5y – 7 = 3x
- Überprüfe rechnerisch, ob der Punkt (5|4,5) auf der zu dieser Gleichung gehörenden Geraden liegt.
- Durch welchen Wert für y wird die Gleichung erfüllt, wenn x = -1 ist.
Gruppe b:
5y – 7 = 3x
- Überprüfe rechnerisch, ob der Punkt (4|4,5) auf der zu dieser Gleichung gehörenden Geraden liegt.
- Durch welchen Wert für y wird die Gleichung erfüllt, wenn x = -1 ist.
a)
Die Gleichung ist eine "lineare" Gleichung, deren Graph im Koordinatensystem
eine Gerade ist. Ohne die Gerade zu zeichnen, kann man durch Einsetzen der gegebenen
Punktkoordinaten in die Gleichung feststellen, ob der Punkt zu der Geraden gehört,
d.h. ob der Punkt auf der Gleichung liegt. Das ist dann der Fall, wenn die Werte
für x und y die Gleichung erfüllen. Bei beiden Gruppen ist das nicht der Fall!
Beim rechnerischen Überprüfen müssen die Koordinaten des Punktes in die Gleichung
eingesetzt werden. Wenn die Gleichung dann nach dem Ausrechnen beider Seiten "stimmt",
so liegt der Punkt auf der Geraden, sonst nicht.
Punkt: (5|4,5) somit ist x = 5 und y = 4,5
5y — 7 = 3x
5·4,5 — 7 = 3·5
22,5 — 7 = 15
15,5 = 15 falsche Aussage!
Þ Punkt liegt nicht auf der Geraden
Punkt: (4|4,5) somit ist x = 4 und y = 4,5
4y — 7 = 2x
4·4,5 — 7 = 2·4
18 — 7 = 8
11 = 8 falsche Aussage!
Þ Punkt liegt nicht auf der Geraden
b)
Um herauszufinden, welcher Wert für y die Gleichung erfüllt, wenn x=-1 ist, müssen die Gleichungen zunächst nach y umgeformt werden. Dann kann man für x -1 einsetzen und das gefragte y ausrechnen. Man kann auch erst einsetzen und dann umformen (siehe Gruppe b).
5y — 7 = 3x | + 7
5y = 3x + 7 | : 5
y = 0,6x + 1,4
Einsetzen:
y = 0,6·(-1) + 1,4
= -0,6 + 1,4
= 0,8
4y — 7 = 2x
Einsetzen:
4y — 7 = 2·(-1)
4y — 7 = -2 | + 7
4y = 5 | : 4
y = 1,25
Gruppe a
Löse das Gleichungssystem durch das Einsetzungsverfahren:
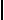
6x + y = 12 -3y – 12x = -21
Da in der ersten Gleichung y keinen Faktor hat, löst man am besten diese erste Gleichung nach y auf und setzt den so gewonnenen Term in die zweite Gleichung für y ein. So erhält man eine lineare Gleichung, die nur noch x und kein y mehr enthält. Mit dieser kann dann x bestimmt werden.
Auflösen von (1) nach y:
6x + y = 12 | - 6x
(1)' y = 12 - 6x
Einsetzen von (1)' in (2):
-3(12 - 6x) - 12x = -21 | Klammer ausmultiplizieren
-36 + 18x - 12x = -21 | x zusammenfassen
-36 + 6x = -21 | + 36
6x = 15 | : 6
x = 2,5
Nun muß noch y berechnet werden, indem der erhaltene Wert für x in die
Gleichung
Einsetzen von x = 2,5 in (1)'
y = 12 - 6x
= 12 - 6·2,5
= 12 - 15
= -3
Gruppe b
Löse das Gleichungssystem durch das Einsetzungsverfahren:
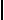
x + 4y = 26 -3y – 4x = -13
Da in der ersten Gleichung x keinen Faktor hat, löst man am besten diese erste Gleichung nach x auf und setzt den so gewonnenen Term in die zweite Gleichung für x ein. So erhält man eine Gleichung, die nur noch y und kein x mehr enthält. Mittels dieser kann zunächst y bestimmt werden:
Auflösen von (1) nach x:
x + 4y = 26 | - 4y
(1)' x = 26 - 4y
Einsetzen von (1)' in (2):
-3y - 4(26 - 4y) = -13 | Klammer ausmultiplizieren
-3y - 104 + 16y = -13 | y zusammenfassen
13y - 104 = -13 | + 104
13y = 91 | : 13
y = 7
Nun muß noch x berechnet werden, indem der erhaltene Wert für y in die
Gleichung
Einsetzen von y = 7 in (1)'
x = 26 - 4y
= 26 - 4·7
= 26 - 28
= -2
Zur Probe müssen die Lösungen in beide Gleichungen eingesetzt werden! Es genügt nicht, nur die Lösungen mit z.B. derjenigen Gleichung zu testen, mit der man am Schluß die zweite Variable bestimmt hat, da sie auch bei einem "falschen" y ein x erzeugt. Diese beiden Werte erfüllen dann die zweite Gleichung, aber nicht die erste!
Bsp. für Probe mit den richtigen Lösungen:
x = -2 y = 7
In (1):
x + 4y = 26
-2 + 4·7 = 26
-2 + 28 = 26
26 = 26 ü
In (2):
-3y – 4x = -13
-3·7 - 4(-2) = -13
-21 + 8 = -13
- 13 = -13 ü
J
Beispiel für Probe mit "falscher" Lösung
Zunächst berechnen wir uns für ein "falsches" y = 5 einen x-Wert:
x = 26 - 4y
x = 26 - 4·5
x = 6
Dann Probe durch Einsetzen in (1):
x + 4y = 26
6 + 4·5 = 26
6 + 20 = 26 ü
Aber nun Probe mit (2):
-3y – 4x = -13
-3·5 - 4·6 = -13
-15 - 24 = -13
-39 = -13 L
Ermittle die Lösung des Gleichungssystems durch das graphische Lösungsverfahren:
Gruppe a: 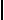
6x – 4y = 10 y = 1 + 1,5x Gruppe b: 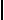
y = 2,5 + 1,5x 6x – 4y = -10
Beim graphischen Lösungsverfahren werden die beiden Gleichungen in einem Koordinatensystem dargestellt. Der Graph einer linearen Gleichung ist eine Gerade, und die Lösung des Gleichungssystems ist der Schnittpunkt der beiden Geraden, denn dieser Punkt liegt auf beiden Geraden und der zugehörige x- bzw. y-Wert erfüllt beide Gleichungen.
Die beiden Gleichungen des Gleichungssystems müssen zur Darstellung im Koordinatensystem
beide in der Form
Gruppe a:
(1) 6x - 4y = 10 | - 6x
-4y = 10 - 6x | :(-4)
y = -2,5 + 1,5x
y = 1,5x - 2,5 (Standardform)
Gruppe b:
(2) 6x – 4y = -10 | - 6x
-4y = -10 - 6x | :(-4)
y = 2,5 + 1,5x
y = 1,5x + 2,5 (Standardform)
Nun hat man die Gleichungssysteme in diese Form gebracht:
(Farben passend zum Graphen unten)
| Gruppe a: | y = 1,5x - 2,5 | |
|
| y = 1,5x + 1 | |||
| Gruppe b: | y = 1,5x + 2,5 | |
|
| y = 1,5x + 2,5 |
Man sieht sofort, daß bei Gruppe b beide Gleichungen identisch sind. Somit liegen die beiden Geraden aufeinander, und es gibt unendlich viele gemeinsame Punkte. Daher gibt es für jedes beliebige x auch ein y, was so ausgedrückt werden kann:
x Î R y = 1,5x + 2,5
Bei Gruppe a ist die Steigung der Geraden m = 1,5 identisch, jedoch das
b, also der Schnittpunkt der Geraden mit der y-Achse verschieden. Somit laufen
die Geraden zueinander parallel und haben keinen Schnittpunkt.
Es gibt daher keine Lösung des Gleichungssystems, was man mit
Graph für beide Gruppen:

Löse das Gleichungssystem durch das Gleichsetzungsverfahren:
Gruppe a: 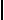
x = 4y + 10 3x – 6y = 15 Gruppe b: 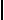
5x – 10 = y 7y – 7x = -14
In beiden Gleichungssystemen steht bereits in jeweils einer Gleichung eine Variable alleine. Die jeweils andere Gleichung kann leicht nach dieser Variablen aufgelöst werden:
(2) 3x - 6y = 15 | + 6y
3x = 15 + 6y | : 3
(2)' x = 5 + 2y
(2) 7y - 7x = -14 | + 7x
7y = -14 + 7x | : 7
(2)' y = -2 + x
Nun werden die rechten Term der Gleichungen des Gleichungssytems jeweils gleichgesetzt, wodurch Gleichungen mit nur noch einer Unbekannten entstehen, die man nach dieser auflösen kann. Danach wird der erhaltene Wert in (1) eingesetzt, um die andere Variable zu ermitteln:
(1) = (2)'
4y + 10 = 5 + 2y | - 2y
2y + 10 = 5 | - 10
2y = -5 | : 2
y = -2,5
Einsetzen in (1)
x = 4y + 10
x = 4·(-2,5) + 10
= -10 + 10
= 0
(1) = (2)'
5x - 10 = -2 + x | - x
4x - 10 = -2 | + 10
4x = 8 | : 4
x = 2
Einsetzen in (1)
y = 5x - 10
y = 5·2 - 10
= 10 - 10
= 0
Gruppe a
Die Summe aus dem Doppelten der ersten Zahl und dem Dreifachen der zweiten Zahl beträgt 73.
Die Summe aus dem Doppelten der zweiten Zahl und dem Dreifachen der ersten beträgt hingegen 67.
Welche Zahlen sind das?
Die beiden Unbekannten sind die beiden Zahlen, denen wir die Variablen x und y zuweisen. Wir stellen das Gleichungssystem auf:
| 2x + 3y = 73 | |
|
| 3x + 2y = 67 |
(1) nach x auflösen:
2x + 3y = 73 | - 3y
2x = 73 - 3y | : 2
(1)' x = 36,5 - 1,5y
(1)' in (2) einsetzen:
3(36,5 - 1,5y) + 2y = 67 | T
109,5 - 4,5y + 2y = 67 | T
109,5 - 2,5y = 67 | - 109,5
-2,5y = -42,5 | : (-2,5)
y = 17
in (1)' einsetzen:
x = 36,5 - 1,5·17
= 11
Gruppe b
Die Summe aus dem Doppelten der ersten Zahl und dem Dreifachen der zweiten Zahl beträgt 61.
Die Summe aus dem Doppelten der zweiten Zahl und dem Dreifachen der ersten beträgt hingegen 49.
Welche Zahlen sind das?
Die beiden Unbekannten sind die beiden Zahlen, denen wir die Variablen x und y zuweisen. Wir stellen das Gleichungssystem auf:
| 2x + 3y = 61 | |
|
| 3x + 2y = 49 |
(1) nach x auflösen:
2x + 3y = 61 | - 3y
2x = 61 - 3y | : 2
(1)' x = 30,5 - 1,5y
(1)' in (2) einsetzen:
3(30,5 - 1,5y) + 2y = 61 | T
91,5 - 4,5y + 2y = 61 | T
91,5 - 2,5y = 61 | - 91,5
-2,5y = -42,5 | : (-2,5)
y = 17
in (1)' einsetzen:
x = 30,5 - 1,5·17
= 5
Gruppe a
Leon hat 7 Kiwis und 1kg Äpfel gekauft und dafür 7,05 DM bezahlt.
Jenny kaufte 5 Kiwis und 1½kg Äpfel für 8,10 DM.
Wieviel müßte man für 5 Kiwis und 1kg Äpfel bezahlen?Gruppe b
Leon hat 7 Kiwis und 1kg Äpfel gekauft und dafür 6,35 DM bezahlt.
Jenny kaufte 5 Kiwis und 1½kg Äpfel für 6,50 DM.
Wieviel müßte man für 5 Kiwis und 1kg Äpfel bezahlen?
Zur Berechnung des gefragten Preises braucht man den Preis für eine Kiwi und den Preis für 1kg Äpfel. Wir setzen also x für den Preis einer Kiwi und y für den Kilopreis der Äpfel.
Die Gleichungssysteme heißen:
| Gruppe a: | 7x + y = 7,05 | |
|
| 5x + 1,5y = 8,1 | |||
| Gruppe b: | 7x + y = 6,35 | |
|
| 5x + 1,5y = 6,5 |
Da y in der ersten Gleichung ohne Faktor erscheint, lösen wir die erste Gleichung nach y auf und setzen den erhaltenen Term für y in die zweite Gleichung ein:
(1) 7x + y = 7,05 | - 7x
y = 7,05 - 7x
in (2) einsetzen:
5x + 1,5y = 8,1
5x + 1,5(7,05 - 7x) = 8,1 | T
5x + 10,575 - 10,5x = 8,1 | T
-5,5x - 10,575 = 8,1 | + 10,575
-5,5x = -2,475 | :(-5,5)
x = 0,45
in (1)' einsetzen:
y = 7,05 - 7x
y = 7,05 - 7·0,45
y = 3,9
Eine Kiwi kostet also 45 Pfennige und ein Kilogramm Äpfel 3,90 DM.
Fünf Kiwis und 1kg Äpfel kosten somit
(1) 7x + y = 6,35 | - 7x
y = 6,35 - 7x
in (2) einsetzen:
5x + 1,5y = 6,5
5x + 1,5(6,35 - 7x) = 6,5 | T
5x + 9,525 - 10,5x = 6,5 | T
-5,5x + 9,575 = 6,5 | - 9,575
-5,5x = -3,025 | :(-5,5)
x = 0,55
in (1)' einsetzen:
y = 6,35 - 7x
y = 7,05 - 7·0,55
y = 2,5
Eine Kiwi kostet also 55 Pfennige und ein Kilogramm Äpfel 2,50 DM.
Fünf Kiwis und 1kg Äpfel kosten somit
Guten Appetit!
Punkteverteilung |
Punkte ® Noten |
Notenspiegel | |||||||||||||||||||||||||||||||||||||||||||||||
|
|
Æ: 3,3 |
Die drei Einser haben zweimal 31 und einmal 29 Punkte. Herzlichen Glückwunsch!
Ich wünsche euch allen schöne, erholsame Ferien!