Lösungen zur 5. Arbeit

Nr. 1  |  Nr. 2  |  Nr. 3  |   Nr. 4  |  Nr. 5  |  Nr. 6  |  Nr. 7  |  Nr. 8  |  Nr. 9
Bewertung und Ergebnis  |  zurück  |  eMail  |  Übersicht Matheseiten  |  Gästebuch

Gruppe A ist rot und Gruppe B blau dargestellt.

Aufgabe 1

Erdboden Fenster im ersten Stock Fenster im Erdgeschoß Haus Leiter Dach rechter Winkel

Eine 3,5m | 3,4m lange Leiter wird an eine Hauswand angelehnt und berührt diese in 2,8m | 3m Höhe.
Wie weit ist der Fußpunkt der Leiter von der Wand entfernt? (Die Wand ist genau vertikal und der Boden waagerecht.)

Gegeben sind die Hypotenuse (Leiterlänge) und eine Kathete des rechtwinkligen Dreiecks, das von der Leiter und den Abschnitten von Boden und Wand, die unter der Leiter liegen, gebildet wird (siehe Zeichnung unten rechts). Nach dem Satz von Pythagoras gilt damit a² = h² + x² und x² = a² - h².

x² = 3,5² - 2,8² = 12,25 - 7,84 = 4,41
x = Ö4,41 = 2,1

x² = 3,4² - 3² = 11,56 - 9 = 2,56
x = Ö2,56 = 1,6

Antwort: Der Abstand zwischen dem Fußpunkt der Leiter und der Hauswand beträgt 2,1m bzw. 1,6m.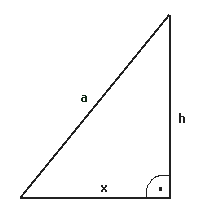

zurück | Seitenanfang

Aufgabe 2

Gegeben sind die drei Punkte A(5|3), B(17|12) und C(0,2|9,4).
Gegeben sind die drei Punkte A(6|2), B(18|11) und C(1,2|8,4).
  a) Berechne die Entfernungen |AB|, |BC| und |AC|!
  b) Überprüfe rechnerisch, ob das Dreieck ABC rechtwinklig ist! (Mit dem Satz des Pythagoras!)

Zu a):
Zunächst müssen jeweils zu zwei Punkten die x- und die y-Abstände berechnet werden, dann kann per Pythagoras die Entfernung berechnet werden:

|AB| = Ö((17-5)² + (12-3)²) = Ö(12² + 9²) = Ö225 = 15
|AC| = Ö((5-0,2)² + (3-9,4)²) = Ö(4,8² + (-6,4)²) = Ö(23,04 + 40,96) = Ö64 = 8
|BC| = Ö((17-0,2)² + (12-9,4)²) = Ö(16,8² + 2,6²) = Ö(282,24 + 6,76) = Ö289 = 17

|AB| = Ö((18-6)² + (11-2)²) = Ö(12² + 9²) = Ö225 = 15
|AC| = Ö((6-1,2)² + (2-8,4)²) = Ö(4,8² + (-6,4)²) = Ö(23,04 + 40,96) = Ö64 = 8
|BC| = Ö((18-1,2)² + (11-8,4)²) = Ö(16,8² + 2,6²) = Ö(282,24 + 6,76) = Ö289 = 17

Zu b):
Ein Dreieck ist genau dann rechtwinklig, wenn die Summe der Kathetenquadrate (Quadrate der beiden kleineren Seiten) gleich dem Quadrat der Hypotenuse (längste Seite) ist. (Umkehrung des Satzes von Pythagoras!)

Es ist also zu prüfen, ob 15² + 8² = 17² gilt; und das ist schnell geschehen: 225 + 64 = 289 = 17². Stimmt. Das Dreieck ABC ist also rechtwinklig!

zurück | Seitenanfang

Aufgabe 3

Berechne den Flächeninhalt des gleichseitigen Dreiecks mit der Seitenlänge 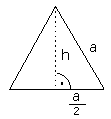a = 6cm!

Die Höhe teilt das gleichseitige Dreieck in zwei kongruente rechtwinklige Dreiecke mit den Katheten h und a/2 sowie der Hypotenuse a. Es gilt also nach Pythagoras: a² = h² + (a/2)² oder mit Zahlen: 6² = h² + 3². Somit ist h² = 6² - 3² = 36 - 9 = 27 und h = Ö27 = 5,19615242270663...

Die Dreiecksfläche berechnet sich mit AD=½·g·h = 0,5·6·Ö27 = 15,5884572681199...

Antwort: Der Flächeninhalt des gleichseitigen Dreiecks mit a=6cm beträgt ca. 15,588cm².

zurück | Seitenanfang

Aufgabe 4

Die Diagonale eines Rechtecks ist 65cm lang. Die längere Seite ist um 13cm | 23cm länger als die kürzere. Berechne den Flächeninhalt des Rechtecks!

Setze x als die kürzere Seite. Dann ist a = x + 13 | a = x + 23 und b = x. Die Unbekannte x kann mit dem Satz des Pythagoras berechnet werden, da die Diagonale d das Rechteck in zwei rechtwinklige Dreiecke zerteilt:

65² = a² + b² = (x + 13)² + x²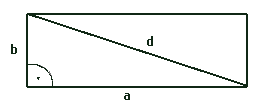
4225 = x² + 26x + 169 + x² = 2x² + 26x + 169    | :2
2112,5 = x² + 13x + 84,5   | - 2112,5
x² + 13x - 2028 = 0
p = 13    q = -2028
x1/2 = -6,5 ± Ö(42,25 + 2028) = -6,5 ± 45,5
Da nur positive Längen in Frage kommen und x1 negativ ist, ist x2 = -6,5 + 45,5 = 39 die gesuchte kürzere Seitenlänge.

65² = a² + b² = (x + 23)² + x²
4225 = x² + 46x + 529 + x² = 2x² + 46x + 529    | :2
2112,5 = x² + 23x + 264,5   | - 2112,5
x² + 23x - 1848 = 0
p = 23    q = -1848
x1/2 = -11,5 ± Ö(132,25 + 1848) = -11,5 ± 44,5
Da nur positive Längen in Frage kommen und x1 negativ ist, ist x2 = -11,5 + 44,5 = 33 die gesuchte kürzere Seitenlänge.

Nun berechnet man für die Berechnung des Flächeninhalts zunächst die längere Seite mit
a = x2 + 13 = 39 + 13 = 52 bzw. a = x2 + 23 = 33 + 23 = 56
und damit ergibt sich A = a·b = 52·39 = 2028 bzw. A = a·b = 56·33 = 1848.

Antwort: Der Flächeninhalt des Rechtecks beträgt 2028cm² | 1848cm².

zurück | Seitenanfang

Aufgabe 5

Bestimme den Definitionsbereich und die Lösungen dieser Bruchgleichung:

Der Definitionsbereich wird eingeschränkt durch diejenigen Werte für x, bei denen ein Nenner Null wird, denn durch Null darf nicht geteilt werden. Dies ist der Fall für x = -2 und x = 16, wie man leicht sieht.
Es gilt damit: D = R \ {-2; 16}    (D: Definitionsbereich, R: Menge der reellen Zahlen)

Lösungen der Gleichung finden durch Umformen der Gleichung und Anwenden der Lösungsformel:
Zunächst mit den Nennern multiplizieren, dabei jeweils gleich vereinfachen, dann in Normalform quadratischer Gleichungen überführen, p und q ablesen und mit der p-q-Formel die Lösungen berechnen:

   5           10
 ————— + 3 = ——————          | ·(x+2)
  x+2         16-x

                 10(x+2)
  5 + 3(x+2) = —————————     | ausmultiplizieren
                  16-x

                 10x + 20
  5 + 3x + 6  = ——————————   | ... und vereinfachen
                   16-x

               10x + 20
  11 + 3x  =  ——————————     | ·(16-x)
                 16-x

  11(16-x) + 3x(16-x) = 10x + 20      | Klammern ausmultiplizieren

  176 - 11x + 48x - 3x² = 10x + 20    | zusammenfassen

  176 + 37x - 3x² = 10x + 20          | - 10x  

  176 + 27x - 3x² = 20                | - 20  

  156 + 27x - 3x² = 0                 | umsortieren

  -3x² + 27x + 156 = 0                | :(-3)

   x² - 9x - 52 = 0

   p = -9       q = -52

   x1/2 = 4,5 ± Ö(20,25 + 52) = 4,5 ± 8,5

   x1 = 4,5 - 8,5 = -4

   x2 = 4,5 + 8,5 = 13
zurück | Seitenanfang

Aufgabe 6

Berechne eine positive Zahl, die sich von ihrem Kehrwert um 5 bzw. 6 unterscheidet.

Setze für die gesuchte Zahl x. Der Kehrwert der Zahl ist dann 1/x.
Da nicht angegeben ist, ob der Kehrwert oder die Zahl selbst größer sein soll, sind alle diese Gleichungen als Ansatz korrekt:

         1                    1         1                  1
 x + 5 = —            x - 5 = —         — + 5 = x          — - 5 = x
         x                    x         x                  x

                                  1                      1
             es ginge sogar    ——————— = x     und    ——————— = x 
                                x + 5                  x - 5

(Bei Gruppe B statt 5 entsprechend 6 einsetzen.)

Ich rechne hier mal die zweite Gleichung vor:

          1
 x - 5 = ———      | ·x     
          x

 x² - 5x = 1      | -1

 x² - 5x - 1 = 0

zur Abwechslung quadratische Ergänzung:

 x² - 5x - 1 = 0  | + 7,25

 x² - 5x + 6,25 = 7,25

 (x - 2,5)² = 7,25    | Ö

  x - 2,5 = -2,69258240356725...       Ú      x - 2,5 = +2,69258240356725...     | + 2,5

  x = 0,19258240356725...  Ú   x = -5,192582403567252...

Probe:
  1 : 0,192582403567252 = 5,19258240356725
  1 : (-5,19258240356725) = -0,192582403567252

Beide Lösungen unterscheiden sich um 5 von ihrem Kehrwert!

Bei Gruppe B führt die analoge Ausgangsgleichung x - 6 = 1/x auf die Normalform x² - 6x - 1 = 0, und das hat die Lösungen x = 6,1622776601...  Ú  x = -0,1622776601...

zurück | Seitenanfang

Aufgabe 7

Begründe, warum das Dreieck ABC rechtwinklig ist mit 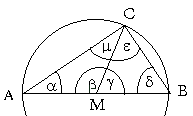m + e = 90°

Die Dreiecke AMC und MBC sind gleichschenklig, da |AM| = |MC| = |MB|.
Diese drei Strecken sind nämlich allesamt Radien des (Halb-)Kreises um M.

Da gleichschenklige Dreiecke zwei gleiche Winkel an der Grundseite haben, gilt: a = m und d = e.

Für die Winkelsumme im Dreieck ABC gilt: a + d + e + m = 180°.

Wenn man nun a und d durch die jeweils gleichen Winkel m und e ersetzt, so ergibt sich:

m + e + e + m = 2m + 2e = 180°    und damit:    m + e = 90° (q.e.d. — Satz des Thales)

Siehe auch das Java-Applet zum Thales-Satz  

zurück | Seitenanfang

Aufgabe 8

Pythagoras und seine Anhänger hatten als Zeichen das Pentagramm. Sie entdeckten darin den goldenen Schnitt.
Zeichne zwei Strecken ein, die zueinander das Verhältnis des goldenen Schnitts bilden.

 

Richtige Lösungen sind beispielsweise:

|AB|:|BC|, |AC|:|AD|, |AB|:|AD|, |EF|:|BC|, |EF|:|CE|, |BE|:|BD|, |AC|:|FE| oder |BE|:|CE|

Alle diese Streckenverhältnisse (und noch viele mehr) betragen 1,618... oder 0,618..., wie man hier lediglich durch Nachmessen und Dividieren der Streckenlängen überprüfen sollte.

Ausprobieren: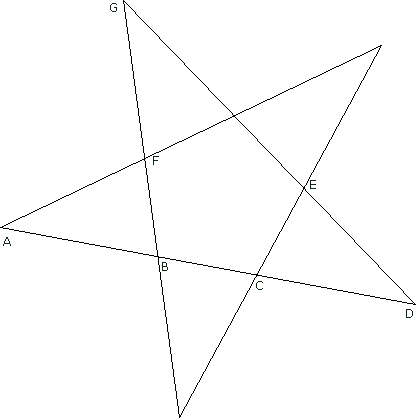

| | : | | =
zurück | Seitenanfang

Aufgabe 9

Zur Darstellung im Internet, wo im Ausschnitt des Botticelli-Tafelbildes überall der goldene Schnitt zu finden ist, brauche ich ein wenig Zeit. Dazu schreibe ich ein Java-Applet, und das dauert einige "Minuten".

Hier aber nochmal das Bild, das ich wirklich ausgesprochen ansehnlich finde...

zurück | Seitenanfang

Bewertung und Ergebnisse

später...