Keplers Gleichung

Lösung der Keplerschen und anderer transzendenter Gleichungen

Auf dieser Seite wird die Lösung der Keplerschen Gleichung x=a+b·sin(x) bzw. ähnlicher transzendenter Gleichungen bis auf 1000 Kommastellen genau berechnet.

Die Anwendung der Keplerschen Gleichung in der Astronomie

Die Gleichung E = µ(t–T) + e·sin(E) stellt den Zusammenhang zwischen der numerischen Exzentrizität e einer Planetenbahn und der exzentrischen Anomalie E zum Zeitpunkt t her. T ist dabei der Zeitpunkt, an dem der Planet im Perihel steht (sonnennähester Punkt der Bahn), µ die mittlere Bewegung (Winkelgeschwindigkeit). Der Term µ(t–T), der oben unserem a entspricht, in astronomischen Berechnungen aber gewöhnlich mit M bezeichnet wird, gibt also den „mittleren“ Winkel an, ein dem der Planet zum Zeitpunkt t von der Bahnmitte aus gesehen zu seinem Perihel steht. Die Gleichung präsentiert sich meist in der Gestalt E – e·sin(E) = M.


	Abbildung 1

Was bedeutet aber „mittlere" Strecke?

Bei einer Kreisbahn (beim Kreis ist e=0) ist E=M. Bei elliptischen Bahnen gilt wegen 0<e<1 offensichtlich E>M, für E<π(=180°) und für E>π ist E<M. Der Summand e·sin(E) ist ein Korrekturglied, das sich umso stärker bemerkbar macht, je exzentrischer die Bahn ist. Da M proportional von t abhängt, wird diese Größe auch mittlere Anomalie genannt.

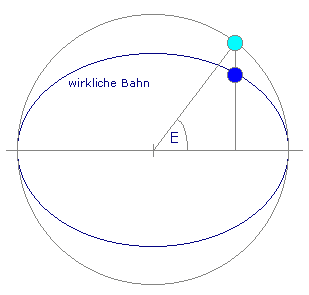
Die Anomalie E ist der Winkel, unter dem der Planet von Mittelpunkt der Bahn-Ellipse aus erscheinen würde, wenn er auf sich einem Kreis mit dem Radius der großen Halbachse der Ellipse bewegen würde und (siehe dazu Abbildung 1) seine Position in Richtung der kleinen Halbachse auf den Kreis projiziert wäre. Diese hypothetische Kreisbewegung ist unregelmäßig: Da sich der Planet in Sonnennähe schneller bewegt als in Sonnenferne eilt er einem gleichmäßig auf dem Kreis fliegenden Planeten mit gleicher Umlaufzeit bis zum sonnfernsten Punkt voraus. M gibt den Winkel an, unter dem ein gleichmäßig auf der Kreisbahn bewegter Planet erschiene, E den Winkel, unter dem die Projektion (hellblau dargestellt) des echten Planeten erscheint.


Abbildung 2

Die wahre Anomalie ν ist der Winkel, unter dem der Planet von der Sonne (d.h. dem Brennpunkt der Ellipse) aus erscheint. Ihn und die Entfernung r kann man mit E berechnen.

Es gelten die Zusammenhänge

ν = 2·atan(√((1+e)/(1-e)) · tan(E/2))

r = a·(1 – e·cos(E))
= a·(1 – e²)/(1 + e·cos(ν))

wobei a die große Halbachse der Ellipse ist.

Animation downloaden
(VB5-Programm)

Im folgenden können Sie das für die Planeten des Sonnensystems, den Kometen Halley und einen selbstdefinierbaren Körper im Sonnensystem ausprobieren. Geben Sie dazu einen beliebigen Zeitpunkt zwischen 1900 und 2100 ein (korrigieren Sie gegebenenfalls die Zeitzone, d.h. die Differenz zu GMT). In der letzten Zeile müssen Sie die Exzentrizität e der Bahn (|e|<1), die Länge ihrer großen Halbachse a und ein Datum für T (Zeit optional, in GMT) angeben.

Datum	Uhrzeit	Zeitzone (Unterschied zur Greenwich Meridian Time in Stunden)
			aktueller Uhrzeit folgen

Planet/ Komet	e	a [Mio km]	Umlauf [Jahre]	µ [1"/s]^*
Merkur	0,2056	57,91	0,24085	0,17050728
Venus	0,0068	108,21	0,61520	0,06675229
Erde	0,0167	149,60	1,00002	0,04106504
Mars	0,0934	227,9	1,88085	0,02183364
Jupiter	0,0484	778,4	11,8626	0,00345999
Saturn	0,0542	1426,7	29,4475	0,00138608
Uranus	0,0472	2871,0	84,0168	0,00047730
Neptun	0,0086	4498,3	164,791	0,00024815
Pluto	0,249	5906,4	247,921	0,00016305
Halley	0,967	2668	75,809	0,00016306

^* Einheit von µ in der Tabelle: Bogensekunden pro Sekunde = (1/3600)° / s

konstant:
	e	numerische Exzentrizität e=√(a²–b²)/a der Planetenbahn, wobei a und b die Achsen der Ellipse sind. (e=0: Kreis, e=1: Parabel)
	a	große Halbachse der Bahn in Millionen km (Abstand des Perihels zum Mittelpunkt der Bahnellipse), kleine Halbachse: b=a√(1–e²)
	Umlauf	Dauer eines Umlaufs um die Sonne in Jahren (bei ungestörter Bahn ist das Quadrat der Umlaufzeit proportional zu a³)
	µ	mittlere Winkelgeschwindigkeit in Bogensekunden pro Sekunde (3600 Bogensekunden = 1 Grad)
veränderlich:
	T	Zeitpunkt (Tag) des letzten Perihel-Durchgangs
	t-T	verstrichene Zeit nach dem letzten Perihel-Durchgang in Sekunden
	M	mittlere Anomalie =µ(t-T) in Grad
	E	exzentrische Anomalie in Grad, gewonnen aus der Keplerschen Gleichung E=M+e·sin(E)
	ν	wahre Anomalie in Grad (Winkel zwischen Perihel- und aktueller Position zum Zeitpunkt t von der Sonne aus)
	r	Abstand des Planeten von der Sonne in Millionen km zum Zeitpunkt t
	v	Bahngeschwindigkeit in km/s zum Zeitpunkt t

Keine Gewähr für die Richtigkeit der Angaben, astronomischen Daten und Berechnungsergebnisse!