Matheseiten-Übersicht  •   zurück  •   weitere Beispiele    Rechner für lin. Gleichungssysteme

Hausaufgaben (Gleichungssysteme 1)

Hier die versprochenen Lösungen der Hausaufgaben. Danke, Michelle!

S. 18, Nr. 9

e)

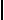	2y = 26 - 4x
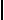	y - 3x = -2

Zum Gleichsetzen mit y werden beide Gleichungen nach y aufgelöst:

    I:      2y = 26 - 4x       | :2
    I':      y = 13 - 2x

    II:      y - 3x = -2       | +3x
    II':          y = 3x - 2

Gleichsetzen und nach x auflösen:
    I'=II':  13 - 2x = 3x - 2  | +2x
                  13 = 5x - 2  | +2
                  15 = 5x      | :5
                   3 = x

Einsetzen in I' zum Berechnen von y:
    in I':   y = 13 - 2x = 13 - 2·3 = 7

Probe (Einsetzen der Lösungen in BEIDE Gleichungen):
    I:       2·7 = 26 - 4·3
             14  = 14         OK
    II:      7 - 3·3 = -2
                 -2  = -2     OK

f)

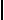	2x + 2y = 148
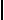	4x + y = 74

Es bietet sich das Einsetzungsverfahren an.
Die II. Gleichung nach y auflösen und in die I. einsetzen:

    II:      4x + y = 74            | -4x
    II'           y = 74 - 4x

    II' in I:    2x + 2y = 148
             2x + 2(74 - 4x) = 148
             2x + 148 - 8x = 148   | -148
             -6x = 0                  | :(-6)
                x = 0
                     (Nicht vor der 0 erschrecken, es ist auch nur eine Zahl.)

    in II':     y = 74 - 4·0 = 74

Probe:
    I:     2x + 2y = 148
           2·0 + 2·74 = 148     
               148 = 148       OK
    II:    4x + y = 74
           4·0 + 74 = 74       OK

g)

	y + 2x = 16
	3y - x + 8 = 0

Diesmal beide nach x auflösen und gleichsetzen.

    I:    y + 2x = 16             | -y
              2x = 16 - y         | :2
    I':        x = 8 - 0,5y

    II:   3y - x + 8 = 0          | +x
    II':      3y + 8 = x

    I'=II':   8 - 0,5y = 3y + 8   | +0,5y -8
                     0 = 3,5y             
                     y = 0

    In II':   x = 8 - 0 = 8

  Probe:
    I:       y + 2x = 16
             0 + 2·8 = 16    OK
    II:    3y - x + 8 = 0
           0 - 8 + 8 = 0     OK

S. 19, Nr. 2

a)

	2x + 5y = 9
	y = 3x + 12

     rechte Seite von II in I für y einsetzen:
              2x + 5y = 9
              2x + 5(3x + 12) = 9
              2x + 15x + 60 = 9      | -60
              17x = -51              | :17
                x = -3

     in II:    y = 3(-3) + 12 = -9 + 12 = 3

  Probe:
     I:     2x + 5y = 9
            2(-3) + 5·3 = 9
            -6 + 15 = 9        OK
     II:    y = 3x + 12
            3 = 3(-3) + 12
            3 = -9 + 12        OK

b)

	4y + x = 24
	y = 6 - 10x

Wieder II für y in I einsetzen:
            4y + x = 24
            4(6 - 10x) + x = 24
            24 - 40x + x = 24     | -24
            -39x = 0      
            x = 0

   In II:   y = 6 - 10x = 6 - 0 = 6

  Probe: 
      I:    4y + x = 24
            4·6 + 0 = 24     OK
      II:   y = 6 - 10x
            6 = 6 - 0        OK

Ein alternativer (aber unvorteilhafter) Ansatz wäre, I nach x aufzulösen 
und in II einzusetzen:
      I:    4y + x = 24           | -4y
            x = 24 - 4y

    in II:  y = 6 - 10(24 - 4y)
            y = 6 - 240 + 40y     | -40y
            -39y = -234           | :(-39)
            y = 6
                
    in I':  x = 24 - 4y = 24 - 4·6 = 0

b)

	y = 1/2·x + 3		(1/2 soll der Bruch "Ein Halbes" sein)
	-4x - 7y = 9

Hier bietet sich natürlich an, die rechte Seite von I für y in II einzusetzen:

      II:   -4x - 7y = 9
            -4x - 7(1/2·x + 3) = 9
            -4x - 3,5x - 21 = 9       | +21
            -7,5x = 30                | :(-7,5)
            x = -4

      in I:  y = 1/2·x + 3 = 1/2·(-4) + 3 = -2 + 3 = 1
 

   Probe:
      I:    y = 1/2·x + 3
            1 = 1/2·(-4) + 3
            1 = -2 + 3          OK
      II:   -4x - 7y = 9
            -4·(-4) - 7·1 = 9
            16 - 7 = 9          OK

© Arndt Brünner, 5. 10. 2003
eMail: arndt.bruenner@t-online.de
Erklärungen zu den Verfahren
Weitere Beispiele mit Lösungen
Rechner für lineare Gleichungssysteme
Übungsaufgaben
Gästebuch
Forum
 
Version: 5. 10. 2003