Logarithmische Spiralen

Matheseitenüberblick
Die Spira mirabilis und weiteres zur logarithmischen Spiralen

Goldene und andere logarithmische Spiralen

Streckfaktor: 2

Tangenten

Logarithmische Spiralen nehmen in ihrem Radius nicht linear zum Drehwinkel zu, sondern exponentiell. Den Zuwachs pro Umdrehung nennt man den Streckfaktor. Entsprechend zieht sich die Spirale nach innen zwar immer mehr zusammen, erreicht aber nie das Zentrum, das man auch Pol nennt.

Die Spiraldarstellung in der Graphik links bricht nach innen hin ab, wenn der Abstand zum Pol kleiner als 1 Pixel wird.

Betrachtet man einen beliebigen Radiusstrahl von Pol aus und ist der Streckfaktor beispielsweise 2, dann verdoppeln sich die Abstände zum Pol für jeden Schnittpunkt mit der Spirale. Und auch die Abstände zwischen den Schnitten verdoppeln sich.
Denn wenn c=2b=4a ist, dann ist b=2a und b-a=2a-a=a sowie c-b=4a-2a=2a.

Das gilt analog und daher allgemein für jeden beliebigen Streckfaktor (>1).

Die logarithmische Spirale wird in jedem Schnittpunkt von jedem beliebigem Radiusstrahl in konstantem Winkel geschnitten, der $90 ° - atan (\frac{ln(q)}{2π})$ beträgt (q: Streckfaktor). Für die aktuell angezeigte Spirale ist das: α≈6,3°.

Probieren Sie es aus, indem Sie mit der Maus ins Graphikfenster zeigen. Der Streckfaktor kann per Schieberegler oder per Mausrad verändert werden.

Spiralen und Rechtecksteilungen

Spirale

x-y-Extrema
Schnitte (oben)

Vergrößerung:

Man kann bei Rechtecken mit dem Seitenverhältnis r:1 stets ein kleineres Rechteck abtrennen, das dasselbe Seitenverhältnis hat. Teilt man das kleinere wieder und auch dieses und so fort, so ziehen sich die Rechtecke immer dichter an einen Punkt zusammen, der s/(1/r²+1) vom linken bzw. oberen Rand des größten Rechtecks entfernt liegt, wobei s die jeweilige Seitenlänge ist.

Die Rechtecke sind sich ähnlich (gleiche Seitenverhältnisse), und deren Kantenlängen wachsen mit konstantem Faktor bzw. nehmen nach innen um diesen ab. Durch ihre äußeren Eckpunkte kann eine logarithmische Spirale gezeichnet werden, deren Streckfaktor die vierte Potenz des Rechteckseitenverhältnisses ist. Betrachten Sie dazu das animierte Bild rechts sowie die interaktive Graphik rechts. Links hat das Außendreieck das Kantenverhältnis des goldenen Schnitts, ist also ein sogenanntes goldenes Rechteck. Rechts ist die Anfangseinstellung ebenso.

Bild sichtbar

Man beachte, daß dabei der Teil des Rechtecks, der nicht weiter geteilt wird, natürlich nicht das ursprüngliche Seitenverhältnis hat. Besondere Fälle sind diesbezüglich das DIN-A-Format, bei dem durch Halbierung der Seiten jede Hälfte wiederum das gleiche Seitenverhältnis (√2:2) hat, sowie wie schon erwähnt das sogenannte goldene Rechteck, bei dem das Verhältnis der längeren zur kürzeren Seite dem Verhältnis des halben Umfangs (also Höhe+Länge) zur längeren Seite gleicht — der Wert ist die Lösung der Verhältnisgleichung $\frac{x + 1}{x} = \frac{x}{1}$ , die äquivalent ist zu x²=x+1, nämlich $x= \frac{\sqrt{5} + 1}{2}$ ≈ 1,618034.
Das ist dann die Länge der langen Rechteckseite, wenn die kurze Seite die Länge 1 hat. Hat die lange Seite die Länge 1, dann hat die größere die Länge $\frac{1}{1,618034...}$ , und das ist interessanterweise genau 1,618034... − 1 = 0,618034....

Bei goldenen Rechtecken verbleibt von jedem goldenen Rechteck durch Abtrennung eines solchen genau ein Quadrat, was eine logische Folge des eben beschriebenen rechnerischen Zusammenhangs ist.

Die Entfernungen der Kurvenpunkte einer logarithmischer Spirale zu ihrem Mittelpunkt nehmen in jeder vollen Umdrehung jeweils um den Faktor r⁴ zu. Dann geht die Spirale durch je zwei diagonal gegenüberliegene Ecken aller Rechtecke. (Pro 360° sind das ja vier Rechtecke, die in ihren Kantenlängen jeweils um den Faktor r wachsen, daher r⁴.)

In vielen populärwissenschaftlichen Darstellungen des goldenen Schnittes wird oft graphisch suggeriert, daß die logarithmische Spirale bei goldenen Rechtecken, die zugehörige Spirale die Rechteckkanten jeweils in den gemeinsamen Ecken benachbarter Rechtecke nur berühre, aber nicht schneide. (Vergleiche das Standbild aus der Terra-X-Sendung Supercodes der Natur, 1. Folge (19'08"), draufklicken zum Vergrößern.)
Das ist allerdings nicht richtig. Wie man in der interaktiven Graphik oben rechts bei entsprechender Einstellung leicht erkennen kann, berührt die Spirale die Kanten von goldenen Rechtecken und ihrer Teilung nicht, sondern schneidet die Kanten.

Die Spirale berührt die Rechteckseiten beim Seitenverhältnis des Rechteckes von r:1 = 1,5388620467909051969...:1, ohne sie zweimal zu schneiden. Dieser Wert ist die Lösung der Gleichung x³·ln(x) = π/2. Das Spiralverhältnis, d.h. der Zunahmefaktor des Radius' pro Umdrehung, ist hierbei r⁴=5,607880555210...

Herleitung:

Logarithmische Spiralen besitzen die allgemeine Polarkoordinatengleichung ρ=a·e^kφ, wobei a eine Konstante ist (beliebiger Vergrößerungsfaktor) und k eine Konstante, die eine Funktion von x ist (siehe unten). In diesem Fall ist ihre Ableitung konstant dρ/dφ=atan(1/k); und damit beträgt der Schnittwinkel τ zwischen Radialen und Spiralkurve eben atan(1/k).

Gewinnung von k aus r: Da der Radius bei einer Umdrehung um den Faktor r⁴ zunimmt, muß gelten:
ρ·x⁴ = a·e^k·(φ+2π) | :x⁴
ρ = a·x^-4·e^k·(φ+2π)
ρ = a·e^{ln(x^-4)}·e^k·(φ+2π)
ρ = a·e^{ln(x^-4)+k·(φ+2π)}
ρ = a·e^{ln(x^-4)+kφ+2πk}
Wegen ρ=a·e^kφ (siehe oben) gilt: kφ = ln(x^-4)+kφ+2πk, und damit ist:
k = -ln(x^-4)/(2π) = 2·ln(x)/π
und der Schnittwinkel τ = atan(π/(2·ln(x))

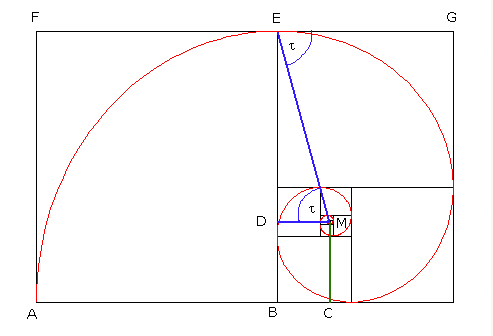
Nun betrachten wir den Fall, daß die Kurve in E die Gerade FG gerade berührt, also ihre Tangente den Winkel τ zur Radialen ME bildet.

Wenn |FG| = x und |AF| = 1, dann ist |AC| = x/(1/x²+1), |DE| = 1/(1/x²+1), |EG| = 1/x, |AB| = x - 1/x und somit |BC| = |AC| - |AB| = x/(1/x²+1) - (x - 1/x) = 1/(x³ + x)

Dann ist tan(τ) = |DE|/|BC| = (1/(1/x²+1))/(1/(x³ + x))=(1/x²+1)/(x³ + x) = x³

Wegen τ=atan(1/k)= atan(π/(2·ln(x⁴)), muß in diesem Falle gelten: π/(2·ln(x)) = x³ oder eben x³·ln(x) = π/2

Selbstähnlichkeit

Logarithmische Spiralen sind selbstähnlich, d.h. eine Drehung hat die gleiche Wirkung wie eine entsprechende Streckung.

In der folgenden Animation wird die Spirale eigentlich gedreht, aber durch die kantenparallel eingefügte Rechteckfolge ist es nicht von einer stetigen Vergrößerung bzw. Verkleinerung zu unterscheiden. Man kann, um diesen Effekt zu reduzieren, die Rechtecke ausblenden.

Rechtecke
Geschwindigkeit:
Spiralverhältnis:

Weiteres...

zu logarithmischen Spiralen, interessante animierte und interaktive Graphiken etc. finden Sie auf →dieser Seite.