Dürers Spinnenlini

Matheseitenüberblick
Dürers Muschellini und zwei andere Kurven

Dürers Spinnenlini

In seiner Unterweysung der Messung (Nürnberg 1525) beschreibt Dürer u.a. die Konstruktion einer Kurve, die der sogenannten Pascalschen Schnecke (siehe →hier) entspricht. Benannt wurde die Pascalschne Schnecke Étienne Pascal (1588-1651, Vater von Blaise Pascal), der diese Kurve 1637, also erst gut hundert Jahre nach Dürer entdeckte. Eine Begründung der Identität von Spinnenlini und (allgemeiner) Pascalscher Schnecke findet sich ↓unten.

ber ein andre lini / die sey genant ein spinnen lini / darum daß sie im aufreissen / dardurch mans macht scheir einer spinnen enlich ist / die mach ich durch ein zwifache bewegung also / Ich reis eyn aufrechte lini a.b. daran setz ich ein andre lini der end sey .c. und die lini a.b. laß ich im end a stet bleiben / Aber das end.b. für ich in zirckels weis herumb / wie ich dann der end im umblauf uberall mit b. verzeichent hab / Darnach soll im end .b. die ander daran gestossen lini .c. mit irem hyndern ende im punckten .b. auch stett bleiben / aber das förder end .c. soll in zirckels weiß herum gefürt werden / So dann die erst lini umgefürt / und die ander anstosset auch sonderlich herum gefürt wirdet / so zeichent das end c. ein sonderliche lini / damit aber dise lini gewyß gefürt werd / so setz ich ein zirckel mit dem ein fuß in dem punckten .a. und reiß mit dem andern fuß eyn zirckellini under dem /b/ die gradir ich auch in theyl mit ziffern / dardurch die lini .a.b. von punckt zu punckt gewyß gee / Des gleichen thue ich im auch im punckten .b. unnd so offt ich mit der lini .a.b. eyn grad gee / so oft gee ich auch ein grad im zirckel .b. mit der lini .c.so zeichnet das end .c. die punckten zwischen den ir lini zusamen soll getzogen werden / die ich uberall mit .c. verzeichent hab / wie das nachfolgett aufgeryssen ist.

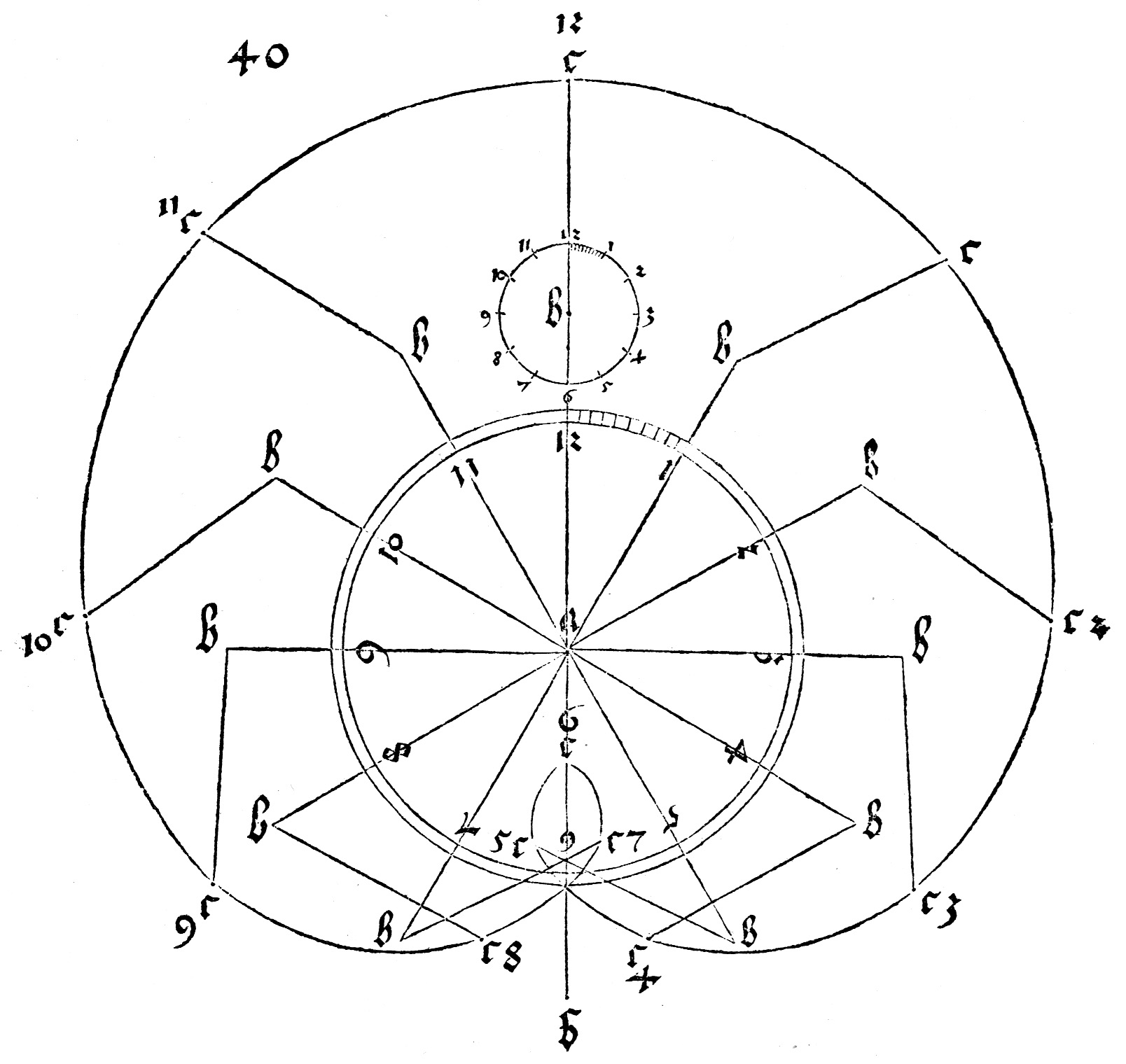
Freie und verknappte Transliteration:
Aber eine andere Kurve, die Spinnen-Linie genannt sei, da sie im Zeichenvorgang einer Spinne ähnelt, mache ich durch eine zweifache Bewegung folgendermaßen:
Ich zeichne eine vertikale Strecke AB. An das Ende B zeichne ich eine weitere Strecke, deren Ende ich C nenne. Nun sei A fest, B aber führe ich im Kreis um A herum. Ich nenne alle diese Punkte B. C wird ebenso im Kreis um B geführt, aber so, daß die Strecke BC ihre Richtung um den selben Winkel gegen AB ändert wie AB gegen die Vertikale gedreht ist. Die Punkte C zeichnen dann eine besondere Linie (Kurve), wie man das in Dürers Zeichnung und der interaktiven Graphik unterhalb dieses Textes sehen kann.

Zur Identität mit der Pascalschen Schnecke

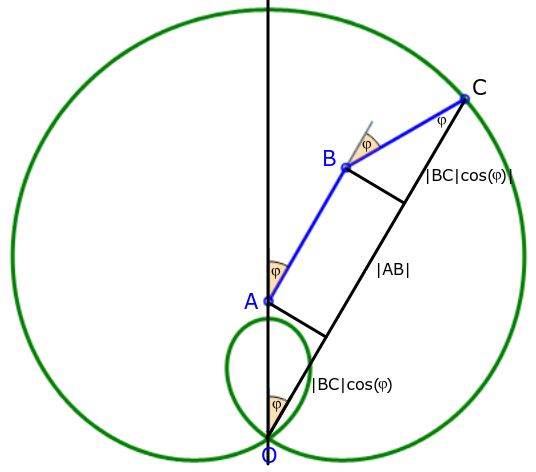
Die Pascalsche Schnecke hat die Polargleichung ρ(φ) = a cos(φ) + b.
(Das ist der Abstand vom Ursprung (Pol) des Kurvenpunktes in Abhängigkeit von der Richtung des Abstandsvektors gegen die x-Achse.)

In der nebenstehenden Abbildung sind eine Parallele zu AB durch C ergänzt und die Lote von A und B auf diese Pararallele. Wegen der Identität der Winkel ist das unten entstehende Dreieck kongruent zum oberen.
So ist ersichtlich, daß hier der Abstand |OC| mit den Bezeichnungen Dürers 2|BC|·cos(φ) + |AB| beträgt, was mit 2|AB|=b und |BC|=a genau in den Abstand aus der Polargleichung übergeht.

Daß O genau in den Zwickel fällt, wenn |OA|=|BC| ist bzw. gewählt wird, wird deutlich aus der Abbildung unten. Das Dreieck CAB ist gleichschenklig mit der Basis AB und dem Basiswinkel α=180°–φ. Wenn φ so groß ist, daß C genau auf der Symmetrieachse liegt, dann kann dorthin O gelegt werden, um die Pascalsche Schnecke mit a=|bc| und b=2|AC| zur Übereinstimmung zu bringen.
Umgekehrt funktioniert Dürers Konstruktion um 90° im Uhrzeigersinn gedreht in der Koordinatensystemdarstellung zur Erzeugung der Pascalschen Schnecke, wenn A(b/2|0), |AB|=b und |BC|=b/2 gewählt wird. Siehe →hier.