Zur Mathematik
Vorbemerkung: Das rechtwinklige Dreieck im Thaleskreis mit der Hypotenuse a (Durchmesser des Thaleskreises) hat bzgl. des Winkels φ die Ankathete a·cos(φ).Siehe Abb. 1.
Daraus ergibt sich sofort einerseits die Polardarstellung der Pascalschen Schnecke
Für
Andererseits erklärt sich dadurch, daß die Abstände P'A und AP konstant gleich b sind, also die Konstruktion der Kurve als die sog. Konchoide des Kreises von einem Pol auf dem Kreis aus.
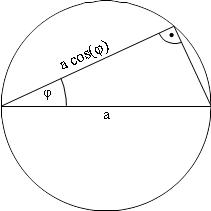 Abb. 1 | 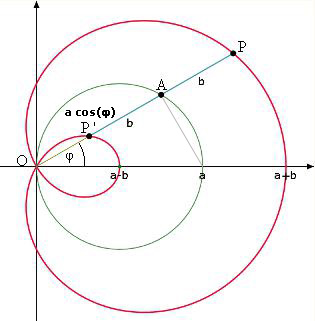 Abb. 2 |
Albrecht Dürer beschrieb, wie eingangs schon erwähnt, in seiner Unterweiung zur Messung (Nürnberg 1515) eine Kurve (Spinnenlini
, siehe
→ hier), die ebenfalls mit der Pascalschen Schnecke identisch ist.
Von einem festen Punkt A aus soll mit fester Länge eine Strecke zum Punkt B gezeichnet werden und von dort mit ebenfalls fester Länge
ein Punkt C, wobei die Richtung um die gleiche Gradzahl gedreht wird, wie schon AB aus der Grundrichtung herausgedreht wurde.
(Dürer nimmt dafür die Vertikale und dreht im Urzeigersinn.)
Mit |AB|=d=a und |BC|=c=b/2 ist |OC| exakt
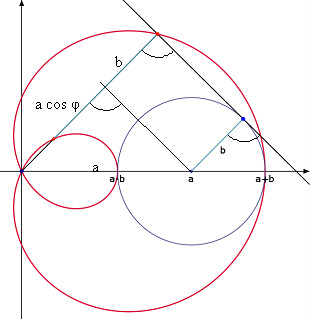 Abb. 3 |  Abb. 4 |
Verallgemeinert man insofern, als dieser Punkt zwar auf der festen Speiche
und dort an fester Stelle bleibt,
also im konstanten Abstand zum Kreismittelpunkt, der aber nicht mehr dessen Radius entsprechen muß, so ergibt sich Dürers
allemeine Konstruktion der Spinnenlinie. (Vergl. Abb. 6 mit Abb. 4)
Der Nachweis, daß die Pascalsche Schnecke auch Enveloppe (Einhüllende) von Kreisen ist,
deren Mittelpunkte auf einem festen Kreis liegen und die durch den Polpunkt O gehen, der selbst nicht auf dem festen
Kreis liegen muß (siehe Abb. 7), ist wesentlich komplizierter.
An dieser Stelle nur zum (einfachen) Zusammenhang zwischen dem Radius dieses Kreises und den Parametern a und b:
Die Kreismitte liege in M(m,0), der Kreis habe den Radius r.
Da die innere Schleife die x-Achse bei a-b schneidet und die äußere Schleife bei a+b (das folgt sofort durch Einsetzen von
φ=0 und φ=π in die o.g. Polargleichung), muß
Für den komplizierteren Rest des Nachweises, der nicht ohne Differentialrechnung auskommen wird,
siehe diese →![]() .
.
Auch zur Winkeldreiteilung durch die Pascalsche Schnecke hier zunächst nur zum wie?
(Siehe Abb. 8)
Falls a=2b ist, kann mit der inneren Schleife der Pascalschen Schnecke ein Winkel gedrittelt werden.
Dazu zeichnet man einen Kreis um O mit dem Radius b (=a/2=a-b). Der Schnitt mit der positiven x-Achse
fällt mit der Nullstelle der inneren Schleife zusammen; der Punkt heiße A. Mit dem Winkel α, den man drittel möchte,
wird gegen die x-Achse gemessen von O aus ein Strahl gezeichnet. Dessen Schnitt mit dem Kreis sei C.
Die Strecke AC schneidet die innere Schleife in B.
Der Winkel ∡AOB drittelt nun den Winkel α=∡AOC.
Einen Beweis findet man in dieser →![]() .
(Etwas simpler wäre schöner — mir fällt aber momentan nichts Simpleres ein. Nebenbei angemerkt will ich mich auch nicht selbst zu arg
im aktuellen Kampf gegen diese netten SarsCov2-Eindringlinge behindern.)
.
(Etwas simpler wäre schöner — mir fällt aber momentan nichts Simpleres ein. Nebenbei angemerkt will ich mich auch nicht selbst zu arg
im aktuellen Kampf gegen diese netten SarsCov2-Eindringlinge behindern.)
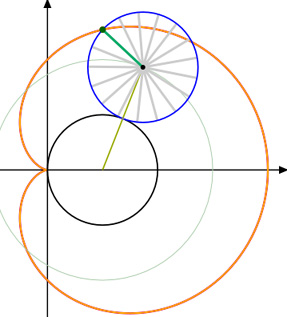 Abb. 5 | 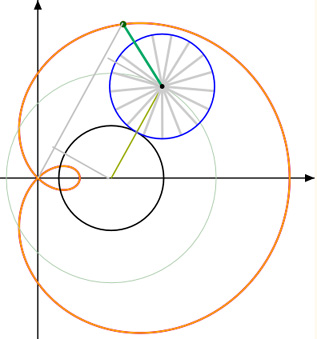 Abb. 6 |
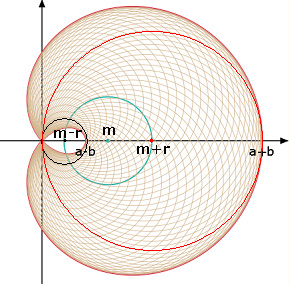 Abb. 7 Abb. 7 |  Abb. 8 |
Da der Radiusvektor r nach der Definition der Pascalschen Schnecke (siehe oben)
Zur
Problematikdes Quadrierens im 4. Schritt sei hier nur angemerkt, daß b·r bzw. r immer genau dann negativ ist, wenn auch x²+y²-ax negativ, also ax>r² ist.
| r = a·cos(φ) + b | | · r |
| r2 = a·r·cos(φ) + b·r | | r2 → x2+y2 und r·cos(φ) → x |
| x2 + y2 = a·x + b·r | | − a·x |
| x2 + y2 − a·x = b·r | | quadrieren |
| (x2 + y2 − a·x)2 = b2·r2 | | r2 → x2+y2 |
| (x2 + y2 − a·x)2 = b2·(x2 + y2) |
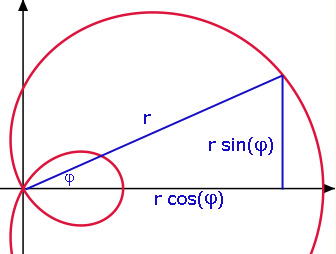
Abb. 9