© Arndt Brünner   •  Matheseitenüberblick   •  Primzahlen etc.   •  zurück   •  zum Tripel-Finder

Pythagoreische Tripel

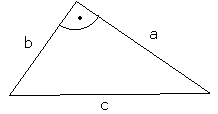
Der Satz des Pythagoras bringt die drei Seitenlängen von rechtwinkligen Dreiecken in den bekannten Zusammenhang:

a² + b² = c²

Hierbei ist c die Seite, die dem rechten Winkel gegenüberliegt (Hypotenuse); und a sowie b sind die Seiten, die den rechten Winkel einschließen (Katheten).

Für die Pythagoreer waren die ganzen Zahlen und ihre Verhältnisse, also die Menge der Rationalen Zahlen, ein Abbild der Welt; in den ganzen Zahlen war das Wesen der Weltschöpfung begründet. Pythagoras war daher blind gegen die Existenz irrationaler Zahlen, die es in dieser Welt nicht geben dürfe. Irrationale Zahlen lassen sich nicht durch Brüche darstellen, als Kommazahl gedacht haben sie unendlich viele Kommastellen, ohne dabei periodisch zu werden! Die Zahl π, die das Verhältnis zwischen Umfang und Durchmesser jeden Kreises angibt, ist ebenso irrational wie die Quadratwurzel aus 2, also diejenige Zahl, die mit sich selbst malgenommen 2 ergibt.

Bemerkenswerterweise ist auch der Goldene Schnitt, bei dem zwei Strecken dasselbe Zahlenverhältnis zueinander haben wie die größere der beiden zur Gesamtstrecke, irrational, nämlich (√5 - 1)/2. Das Pentagramm, in dem dieses Verhältnis eine beherrschende Rolle einnimmt, gilt jedoch als das zentrale Symbol der Pythagoreer. Man kann den goldenen Schnitt (0,618033988749895...) zwar wunderbar durch das Verhältnis zweier aufeinanderfolgender Zahlen der sogenannten Fibonaccifolge approximieren, bei der jedes Folgeglied die Summe seiner zwei Vorgänger ist (1/1 - 1/2 - 2/3 - 3/5 - 5/8 - 8/13 - 13/21 - 21/34 ...), aber nie genau durch einen Bruch angeben. Siehe auch: Approximation von Dezimalzahlen durch Brüche.

Euklid konnte beweisen, daß √2 kein Bruch sein kann, indem er annahm, daß es doch so sei und dadurch einen Widerspruch erhielt:
Wenn a/b=√2, dann ist a²/b²=2. a und b sind dabei natürliche Zahlen, und der Bruch soll vollständig gekürzt sein. Es gilt dann: a²/2=b². Somit ist a² offensichtlich durch 2 teilbar. Dies heißt, daß in der Primfaktorzerlegung von a² die 2 vorkommen muß. In der Primfaktorzerlegung einer Quadratzahl a² sind aber stets die Primfaktoren der Zahl a doppelt enthalten; also muß in a² auch die 2 mindestens doppelt enthalten sein. Mit anderen Worten: Wenn die Quadratzahl gerade ist, muß es auch die Zahl selbst sein.
Da a also gerade ist, kann man sie ersetzen durch a = 2c, wobei c die Hälfte von a ist. Es ist also 2c/b = √2 und 4c²/b² = 2. Dies kann man umformen zu b²/c² = 2. Aus o.g. Gründen muß nun b² gerade sein und man kann die analoge Umformung anwenden, bis man zum Ergebnis c²/d² = 2 kommt, wobei d die Hälfte von b ist. Nun ist der ursprüngliche Bruch, der als vollständig gekürzt vorausgesetzt wurde, doch gekürzt worden. Letztlich könnte man den beschrieben Prozeß bis in alle Ewigkeit fortsetzen und müßte so zu immer einfacheren Brüchen kommen. Da dies ein Widerspruch ist, kann es keinen Bruch a/b=√2 geben!

Nun gibt es für die Gleichung a² + b² = c² auch Lösungen mit ganzen Zahlen, z.B. 3² + 4² = 5² oder 5² + 12² = 13² oder 152² + 285² = 323². Schon in der Antike war bekannt und bewiesen, daß es unendlich viele ganzzahlige Lösungen der Gleichung gibt. Drei ganze Zahlen, die diese Gleichung erfüllen, nennt man Pythagoreisches Tripel.

Für höhere Exponenten als 2, also für a³ + b³ = c³,  a⁴ + b⁴ = c⁴ usw., sucht man bis heute vergebens nach auch nur einem Beispiel eines ganzzahligen Tripels. Im 17. Jahrhundert stellte Pierre de Fermat die Vermutung auf, daß es kein derartiges Tripel geben könne, wenn der Exponent größer als 2 sei, und behauptete auch, es beweisen zu können. Allerdings fand man weder einen Beweis von ihm noch von anderen, die sich rühmten, einen gefunden zu haben, und es dauerte trotz größter Bemühungen namhaftester Mathematiker bis 1994, bis vom Mathematiker Andrew Wiles in Princeton ein allgemein anerkannter, jedoch außerordentlich komplizierter, tiefgründiger Beweis dieses Satzes vorgelegt wurde. Für einige Spezialfälle mit kleineren Exponenten wurde der Satz allerdings schon viel früher bewiesen; auf diesen Seiten findet sich beispielsweise der Beweis von Leonhard Euler für den Fall a³ + b³ = c³, der auch mit solidem Basiswissen gut nachvollzogen werden kann. → Siehe hier.

Auf dieser Seite geht es aber vor allem darum, wie man Pythagoreische Zahlentripel konstruiert, namentlich wenn bereits ein Wert gegeben ist. Am Ende der Seite findet sich ein Formular, mit dem Tripel zu einem bereits gegebenen Wert per Javascript gefunden werden können.

Ein sehr altes Verfahren

Durch folgenden "Trick", der wahrscheinlich schon den Babyloniern (lange vor Pythagoras) bekannt war, kann man beliebig viele dieser Tripel konstruieren und somit gleichzeitig zeigen, daß es unendlich viele pythagoreische Tripel gibt:

Setze	a := m2 - n2
und	b := 2mn

Dann ist:	c2	= a2 + b2
		= (m2 - n2)2 + (2mn)2
		= m4 - 2m2n2 + n4 + 4m2n2
		= m4 + 2m2n2 + n4
		= (m2 + n2)2
und	c	= m2 + n2

Für beliebige Werte für m und n (m, n ∈IN und m > n) lassen sich also pythagoreische Tripel erzeugen:

Man sieht aus dem Term 2mn, daß nach diesem System offensichtlich immer zumindest eine der beiden Katheten gerade werden muß. Kann es nicht auch Tripel mit zwei ungeraden Katheten geben? Vielleicht erfaßt das Verfahren ja nicht alle Möglichkeiten.

Zur Beantwortung dieser Frage ist es zunächst einmal hilfreich, sich folgendes Schema der Differenzen zwischen Quadratzahlen anzuschauen:

Die Differenzen benachbarter Quadratzahlen sind immer ungerade und wachsen um 2. Nehmen wir an, in der Gleichung a² + b² = c² sei b<a. (Falls nicht, kann man die Summanden einfach umtauschen.) b² ist dann die Differenz aus c² und a². Wenn die Quadrate gerade (ungerade) sind, sind es auch die Basen. Dann gibt es folgende Fälle:

Im einzigen Fall, bei dem a² und b² ungerade sind, muß c² gerade sein.

Gerade Zahlen lassen sich als 2n darstellen und ungerade als 2n+1. Im zu betrachtenden Fall sind a und b ungerade, da auch ihre Quadrate ungerade sind. Wir setzen: a=2p+1 und b=2q+1.
c ist gerade, also sei c=2r.

a² + b² = c²

(2p+1)² + (2q+1)² = (2r)²

4p² + 4p + 1 + 4q² + 4q + 1 = 4r²

4p² + 4q² + 4p + 4q + 2 = 4r²

Nach Dividieren durch 4...

p² + q² + p + q + 0,5 = r²

... ergibt sich ein Widerspruch: p, q und r sind ganze Zahlen, somit ist einerseits p² + q² + p + q und andererseits r² ganzzahlig. p² + q² + p + q + 0,5 kann aber wegen des gebrochenen Summanden nicht ganzzahlig sein! Also gibt es den Fall mit a und b ungerade nicht.

Finden von Pythagoreischen Tripeln zu gegebenen Katheten oder Hypotenusen

Man kann das oben genannte Verfahren dazu verwenden, zu gegebenen (ganzzahligen) Katheten (a oder b) alle möglichen Tripel zu finden. Es gibt ein (weiter unten beschriebenes) einfacheres und praktikableres Verfahren, aber zunächst soll auf das bekannte eingegangen werden.

Die gegebene Zahl muß entweder m²-n² oder 2mn sein, wobei m und n natürliche Zahlen sind. Falls die gegebene Kathete ungerade ist, kann es nur der erste Fall sein (m²-n²), sonst kommt in erster Linie der zweite in Frage (2mn), doch bleibt zu prüfen, ob und wann auch m²-n² gerade Differenzen ermöglicht.

Fall 1 — ungerade

Gegeben ist a = m²-n². Betrachten wir noch einmal die schon erwähnte Differenzentabelle:

Hier finden sich zu jeder ungeraden Differenz >1 zwischen Quadratzahlen direkt passende m und n. Wenn a beispielsweise 15 ist, findet man sofort m=8 und n=7 mit m²-n²=15. Allgemein ist m=(a+1)/2 und n=(a-1)/2.

Allerdings läßt sich die Differenz 15 auch durch die drei aufeinander folgenden Differenzen 3, 5 und 7 zusammensetzen, d.h. auch m=4 und n=1 ergibt m²-n²=15. Wenn a=95, dann ist sowohl m=48 und n=47 als auch m=12 und n=7 möglich. Denn 95=19·5=15+17+19+21+23, und dies sind die Differenzen zwischen 7² und 12².

Tatsächlich funktioniert das für alle Fälle, in denen (das ungerade) a in zwei (ungerade) Faktoren p und q zerlegt werden kann. Sei p>q, dann ist n = (p-q)/2 und m = (p+q)/2.

Fall 2 — gerade

Hier können zunächst passende m und n aus dem Zusammenhang b=2mn gefunden werden. Die gegebene Größe wäre dabei also b. Wegen a=m²-n² muß aber m>n gelten. Bei b=24 findet man (m=12,n=1); (m=6, n=2) und (m=4, n=3).

Falls die gegebene Zahl durch 4 teilbar ist, lassen sich m und n auch aus dem ersten Term m²-n² gewinnen: Um gerade Differenzen zweier Quadratzahlen zu erhalten, muß ein geradzahliger Abstand vorliegen, denn die Einzeldifferenzen zwischen den Quadraten sind ungerade, und nur eine Summe aus einer geraden Anzahl ungerader Summanden ergibt eine gerade Zahl. Für a=24 wären das 11+13 (n=5, m=7) und 3+5+7+9 (n=1, m=5). Der erste Fall (11+13) beruht auf der Zerlegung 24=12·2, der zweite auf 24=6·4; jeweils liegt der größere Teiler in der Mitte der Summanden, und der kleinere Teiler gibt die Zahl der Summanden an. Rechts und links der Mitte müssen aber gleich viele Summanden liegen. Somit müssen beide Teiler gerade und damit a durch 4 teilbar sein.

Es lassen sich mit dem vorgestellten Verfahren also diese rechtwinkligen und ganzzahligen Dreiecke mit einer Kathete=24 finden:

Es gibt allerdings noch die beiden Fälle 18² + 24² = 30² und 45² + 24² = 51², die sich nicht direkt mit diesem Verfahren finden lassen. Sie sind jedoch Vielfache der Gleichungen 3² + 4² = 5² (m=2, n=1) bzw. 15² + 8² = 17² (m=4, n=1).

Bessere Dienste tut das...

Verfahren des indischen Mathematikers Brahmagupta

Das 628 geschriebene Lehrwerk Brahmasphutasiddhanta beschäftigt sich hauptsächlich mit Astronomie, enthält aber auch zwei mathematische Kapitel. In Aufgabe 35 des 12. Kapitels (Gantitadhyäya - Arithmetik) gibt Brahmagupta die folgende Regel zur Gewinnung pythagoreischer Tripel aus der gegebenen Kathete a.
(Leicht abgewandelt zitiert nach: H. Gericke, Mathematik in Antike und Orient, Wiesbaden 1992):

Die Seite a des Dreieckes sei beliebig angenommen. Man teile a² durch eine beliebige Zahl d. Dann sind (a²/d - d)/2 = b und b + d = c die beiden anderen Seiten des Dreiecks.

Natürlich muß d ein Teiler von a² sein, wenn die Lösung ganzzahlig sein soll. Um den Zusammenhang mit dem Satz von Pythagoras zu zeigen, wird zunächst b + d = c nach d aufgelöst und in (a²/d - d)/2 = b eingesetzt:

b + d = c

d = c - b

(a²/(c - b) - (c - b))/2 = b

a²/(c - b) - (c - b) = 2b

a²/(c - b) - (c - b)²/(c - b) = 2b

a² - (c - b)² = 2b(c - b)

a² - (c² - 2bc + b²) = 2bc - 2b²

a² - c² + 2bc - b² = 2bc - 2b²

a² - c² - b² = - 2b²

a² - c²= - b²

a² + b² = c²

Da man b durch (a²/d - d)/2 erhält, können für d alle Teiler von a² verwendet werden, für die a²/d - d gerade ist.
c berechnet sich einfach aus b + d.

1. Beispiel: a=24

Es sollen die pythagoreischen Tripel für a=24 als Beispiel für eine gerade Zahl nach dem Verfahren von Brahmagupta berechnet werden. Vergleiche mit den Ergebnissen aus dem ersten Verfahren!

d (Teiler von a2 = 576)	a2/d - d	gerade	b	c	a2 + b2 = c2
1	575
2	286	×	143	145	242 + 1432 = 1452
3	189
4	140	×	70	74	242 + 702 = 742
6	90	×	45	51	242 + 452 = 512
8	64	×	32	40	242 + 322 = 402
9	55
12	36	×	18	30	242 + 182 = 302
16	20	×	10	26	242 + 102 = 262
18	14	×	7	25	242 + 72 = 252
24	0	×	0	24

Bei diesem Verfahren werden also alle sieben Fälle direkt ermittelt.

2. Beispiel: a=315

Beispiel für eine ungerade Zahl nach dem Verfahren von Brahmagupta.

Bei ungeradem a sind nicht nur alle Teiler d ungerade, sondern auch a²/d, denn auch nach Kürzen eines ungeraden Faktors bleiben nur ungerade Primfaktoren. a²/d - d muß dann gerade sein. Daher klappt das Verfahren bei ungeradem a für alle Teiler d<a. Bei d=a wird b = a²/d - d = 0, und bei d>a wird b negativ. Diese Fälle interessieren hier nicht. Teilermengen können übrigens auf der Primzahlseite berechnet werden.

Ermitteln der Katheten zu gegebenem c

Das Verfahren eignet sich leider weniger gut zum Ermitteln von Tripeln zu gegebenem c. Aber es bietet gegenüber dem Ausprobieren doch u.U. erhebliche Geschwindigkeitsvorteile.
Dazu wird in a² + b² = c² das b ersetzt durch c - d:

a² + (c - d)² = c²

a² + c² - 2cd + d² = c²

a² = 2cd - d²

a² = (2c - d)·d

Falls (2c - d)·d für ein bestimmtes d eine Quadratzahl ergibt, erzeugt dieses d ein Tripel.
b wird wieder berechnet mit b = c - d.

Beispiel c = 85

Da sich die Angelegenheit bezüglich a und b symmetrisch verhält, genügt es, b>a anzunehmen, um alle Lösungen zu ermitteln. Aus b>a folgt c-d>a bzw. (c-d)²>a², d.h. (c-d)²>(2c-d)·d und daher d<c·(1-√2/2) ~ 0,292893·c, d.h. im Fall c=85 reicht es, d bis 24 zu testen.

Bei Eingabe eines Dezimalbruchs sucht das Programm nach Tripeln aus Dezimalzahlen mit maximal so vielen Kommastellen, wie die eingegebene Zahl hat. Diese Zusatzfunktion ist sehr hilfreich zur Erstellung von Aufgaben zum Satz des Pythagoras. Es ist möglich, am Schluß durch "überflüssige" Nullen die Anzahl der Dezimalen zu erhöhen. Bei Eingabe von 5,0 wird z.B. 1,4² + 4,8² = 5² gefunden. Achtung: Berechnet wird mit der entsprechenden, mit Zehnerpotenzen erweiterten Ganzzahl, die damit sehr groß werden kann.

Dieses Programm greift auf das gleiche Primzahl- und Primfaktor-Script wie die Primzahl-Seite zurück. Es zerlegt die eingegebene Zahl a in Primfaktoren, um die Teilermenge von a² zu bestimmen. Das geht zwar in der Regel ziemlich schnell, kann aber längere Zeit in Anspruch nehmen, wenn zunächst die interne Primzahltabelle erweitert werden muß, insbesondere wenn a einen oder mehrere große Primfaktoren besitzt. Sobald das geschehen ist, wird auf die gespeicherten Primzahlen zugegriffen, was wieder sehr schnell geht. Leider wird der Speicher durch den Browser beim Verlassen der Seite gelöscht, so daß die Primzahlen nicht erhalten bleiben. Um das zu verhindern, kann ein Link gegebenenfalls in einem neuen Browserfenster geöffnet werden. Dadurch bleiben Seiteninhalt und interne Tabelle im Speicher.

© Arndt Brünner, Gelnhausen, 10. 10. 2001
Version: 16. 11. 2003
Matheseitenüberblick
zurück